 Il "cacciatore" di Spie
Il "cacciatore" di Spie
 Il "cacciatore" di Spie
Il "cacciatore" di Spie
In Grid 90,
la cattura di ogni accadimento spia, di qualunque fenomeno estrazionale, di
qualsivoglia evento numerico trova amplissima trattazione nel modulo "Spie",
raggiungibile sia cliccando sulla omonima voce del
menù laterale,
sia attingendo al menù in alto (Sezione spie) alla voce "Spie statistiche":
Ritorneremo a scuola quando, con penna ...e calamaio, eravamo intenti a
risolvere
espressioni ove
A + B = 12,
col valore della prima o seconda incognita conosciuto.
Ecco un elenco estremamente semplificato degli accadimenti spia catturabili:
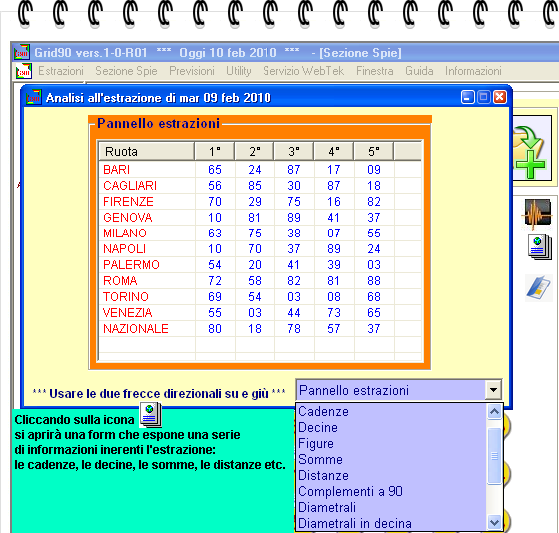
 Ecco lo screenshot
che ci apparirà ad apertura del modulo
Ecco lo screenshot
che ci apparirà ad apertura del modulo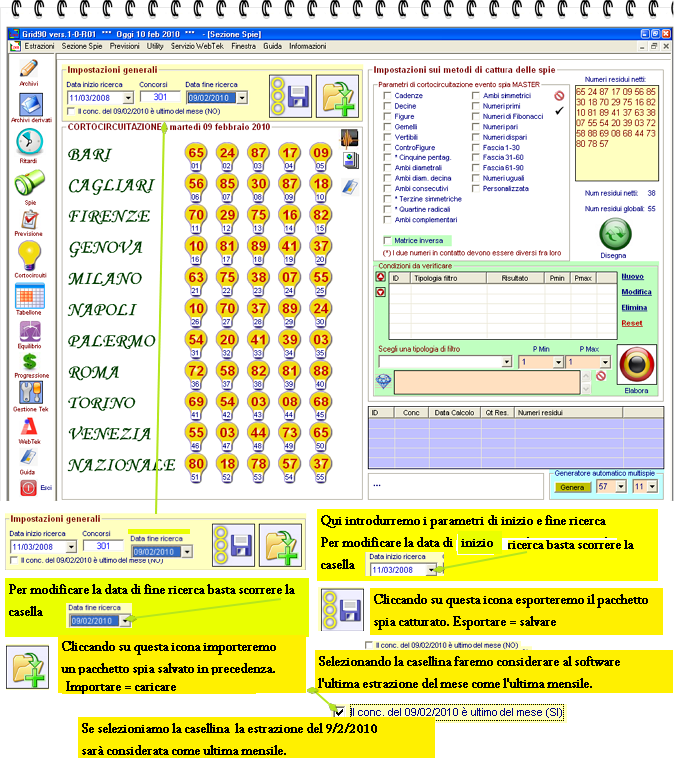

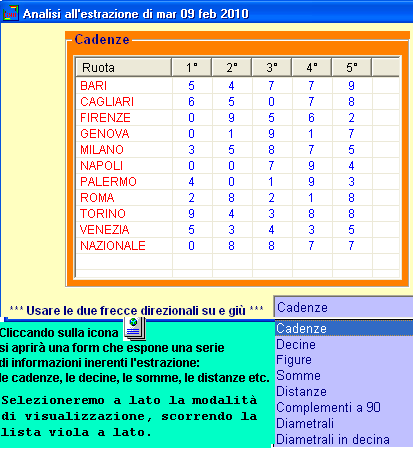
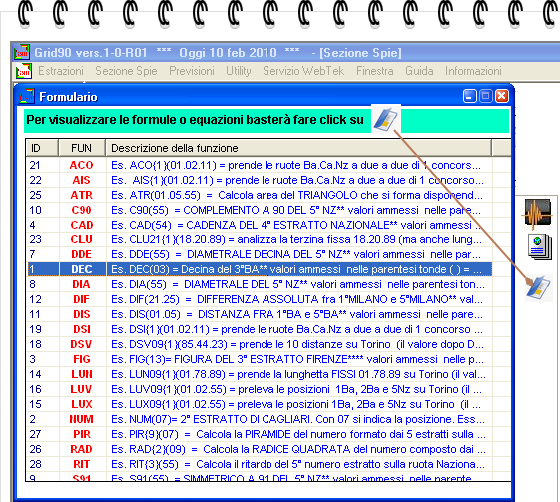
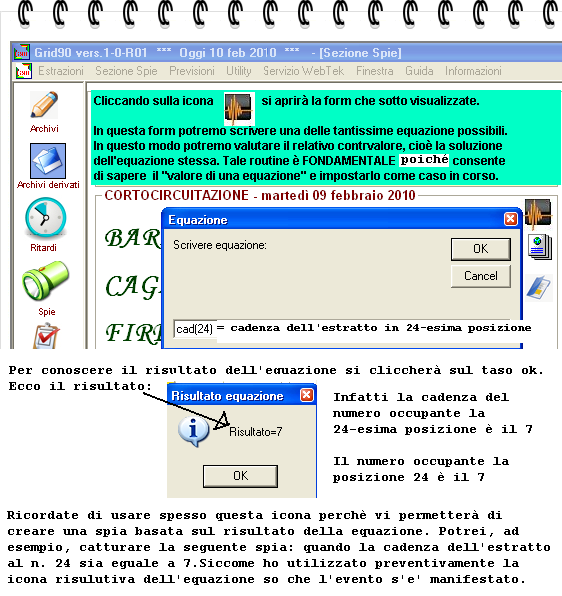
Il tester delle equazioni
usatelo con
frequenza poiché vi agevola nella intercettazione delle spie complesse,
liberandovi dal grosso lavoro manuale necessario a individuare il valore da
attribuire ad una formula. Il tester è un solutore equazionale, è uno
strumento che restituisce un valore che rappresenta la soluzione di quanto
scriviamo nella form:
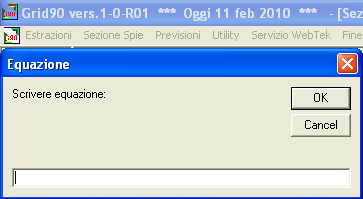
![]() Nella
riga bianca è ammessa la scrittura di ogni tipo di equazione, che poi
ci sarà utile per determinare se un evento spia sia in corso o non sia in
corso.
Nella
riga bianca è ammessa la scrittura di ogni tipo di equazione, che poi
ci sarà utile per determinare se un evento spia sia in corso o non sia in
corso.
Ecco di seguito alcuni esempi basati sulla estrazione del 9 febbraio 2010.
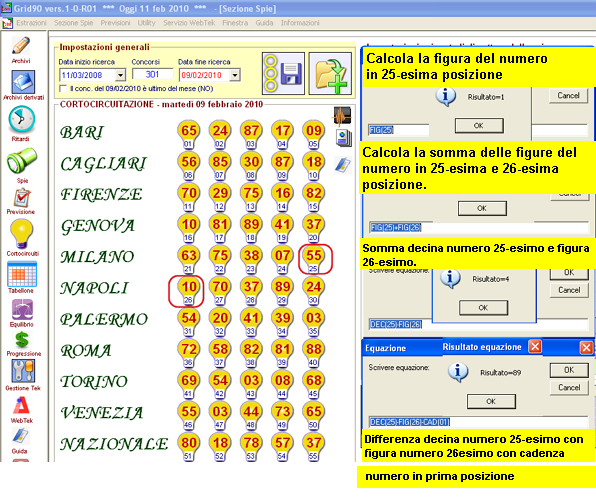
![]() Il
tester equazionale ammette formule multiple, concatenate, vere e proprie
espressioni algebriche delle quali ci farà conoscere il risultato. E cosa ne
faremo noi del risultato, potreste pensare e son sicuro che lo state
pensando?
Il
tester equazionale ammette formule multiple, concatenate, vere e proprie
espressioni algebriche delle quali ci farà conoscere il risultato. E cosa ne
faremo noi del risultato, potreste pensare e son sicuro che lo state
pensando?
Se noi sappiamo che la differenza fra la decina del numero posizionato in prima posizione, corrispondente al 1° di Bari e la cadenza del numero posizionato in 55-esima posizione, che corrisponde al 5° estratto della Nazionale, fornisce come risultato 22, allora potremo scrivere tale equazione nella griglia di cattura reale dell'evento spia.
![]() Sia
data la formula:
FIG(25)+FIG(26) = 2. Sappiamo che nell'ultima estrazione
la figura del numero estratto in 25-esima posizione,
corrispondente al
5° di Milano, + la figura del numero estratto in 26-esima posizione, corrispondente al 1° di Napoli, è eguale a due.
Sia
data la formula:
FIG(25)+FIG(26) = 2. Sappiamo che nell'ultima estrazione
la figura del numero estratto in 25-esima posizione,
corrispondente al
5° di Milano, + la figura del numero estratto in 26-esima posizione, corrispondente al 1° di Napoli, è eguale a due.
Scriviamo questa formula nella griglia di cattura degli eventi
spia
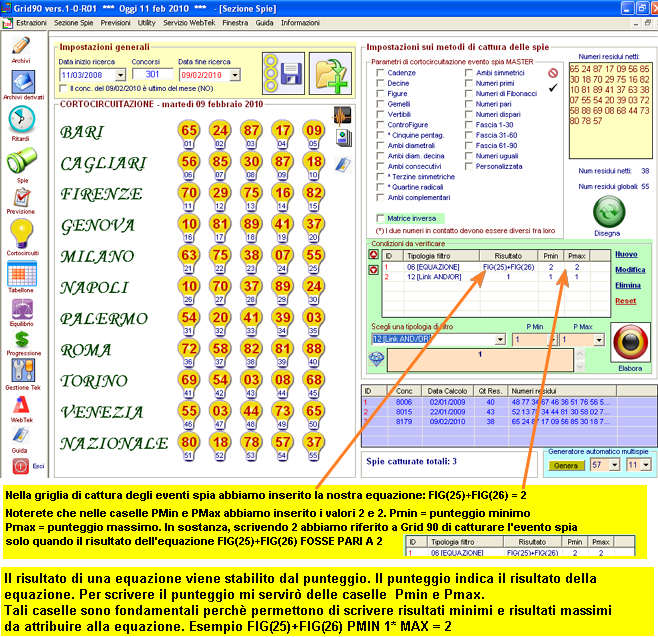
Quindi abbiamo
imparato almeno una funzione importante:
PMin = punteggio(Presenza) minimo *** PMax = Punteggio
(Presenza) massimo.
Il punteggio minimo indica il valore minimo che vogliamo attribuire alla
soluzione della equazione, mentre il punteggio massimo è il valore massimo
che vogliamo attribuire alla soluzione dell'equazione.
Altri esempi occorrono perchè alcuni potrebbero avere la testa dura"...comme 'e serece 'e casa Carrella"
(serece = Pietra dura lavica vesuviana).
Evento spia : SQR(05)-DIS(01.05)+DIF(21.25) = da
67 a 77.
 Significato:
Significato:
Catturami l'evento quando la radice quadrata del numero estratto
in quinta posizione(corrispondente al 5° di Ba)
meno la distanza fra il numero estratto in
prima posizione e il numero estratto in quinta posizione ( 1° e 5°
estratti di Bari) più la
differenza intercorrente fra il numero estratto in posizione 21-esima e il
numero estratto in posizione 25-esima (corrispondenti
rispettivamente al 1° e 5° estratto di Milano)
restituisca un valore compreso fra 67 e 77,
cioè minimo 67 e massimo 77.
Noterete come PMin e PMax acquisiscano un significato di range di possibili
valori, range di possibili risultati attribuibili alla equazione. Questo
criterio è riferibile ad una qualsiasi espressione
utilizzata.
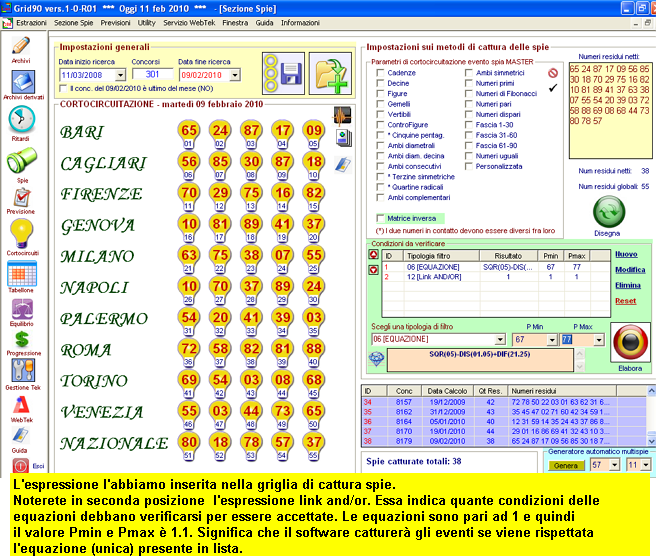
![]() Chiariamo il significato della voce Link and/or
Chiariamo il significato della voce Link and/or
Nella griglia di cattura degli eventi spia possiamo scrivere quante equazioni e formule desideriamo. Poniamo che ne inserissimo 4. Con il controllo Link and/or possiamo chiedere a Grid 90 di catturare gli eventi spia quando tutte e 4 le equazioni o formule siano state verificate, oppure che almeno due delle equazioni o formule siano verificate.
Schematicamente la situazione potrebbe rappresentarsi come segue:
Equazioni e formule = 4 . Vediamo i valori assumibili dal controllo Link and/or:
Link and/or valori PMin Pmax
1 2 significa che minimo 1 max 2 delle equazioni debbano essere verificate
1 3 significa che minimo 1 max 3 delle equazioni debbano essere verificate
1 4 significa che minimo 1 max 4 delle equazioni debbano essere verificate
2 2 significa che minimo 2 max 2 delle equazioni debbano essere verificate
2 3 significa che minimo 2 max 3 delle equazioni debbano essere verificate
2 4 significa che minimo 2 max 4 delle equazioni debbano essere verificate
3 3 significa che minimo 3 max 3 delle equazioni debbano essere verificate
3 4 significa che minimo 3 max 4 delle equazioni debbano essere verificate
4 4 significa che minimo 4 max 4 delle equazioni debbano essere verificate, cioè tutte.
La struttura di controllo Link and/or dovrà essere sempre presente nella griglia di cattura degli eventi spia, qualunque tipo di equazione o formula inserissimo.
![]() La griglia di catturare degli eventi spia
La griglia di catturare degli eventi spia
Per catturare gli eventi spia dobbiamo dapprima inserire le formule e le equazioni nella griglia che le accoglie. Questo lo screenshot:
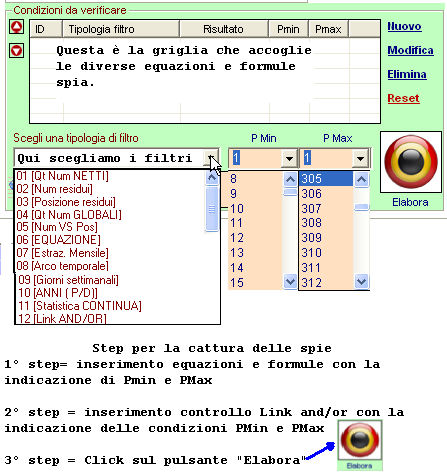
E' importante comprendere, fin d'ora, gli step, le azioni da compiere per la cattura degli eventi spia, così come descritti nella immagine sopra visualizzata.
![]() Le varie tipologie di filtro della griglia cattura-spie
Le varie tipologie di filtro della griglia cattura-spie
 Filtro Equazioni
(Equazione)
Filtro Equazioni
(Equazione)
...e qui si sprofonda in galassie di interminabili stelle ove ciascuna
conduce all'infinito.
Le possibili formule,
equazioni, espressioni sono così incommensurabili che 1000 pagine
non basterebbero a darne la meritata contezza. In
termini quantistici, questa funzione ci assicura la cattura di così tanti
accadimenti del quadro estrazionale da rischiare la buassaggine mentale, l'
inscimunimento cognitivo.
![]() Potremo usare
formule singole;
Potremo usare
formule singole;
![]() potremo far uso di
formule multiple;
potremo far uso di
formule multiple;
![]() potremo far uso di
formule nidificate;
potremo far uso di
formule nidificate;
![]() potremo combinare
le formule in ogni modo.
potremo combinare
le formule in ogni modo.
Inserimento del filtro
estrazioni:
La modalità più semplice di scrivere le equazioni è servirsi del TASTIERINO
EQUAZIONALE.
Ad esso si accede facendo click sulla icona Diamante. Siete di curiosi di
vedere come sia fatto?
Vi accontenterò:
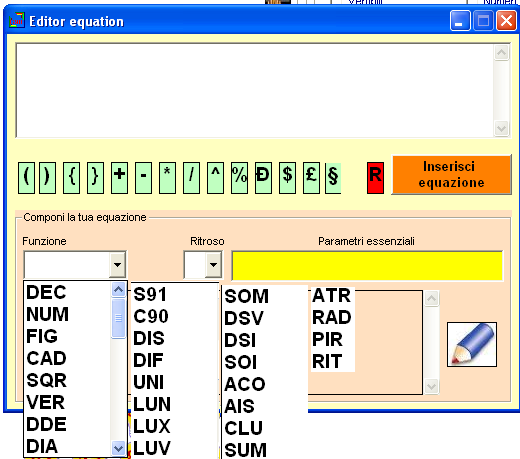
 Esempio di
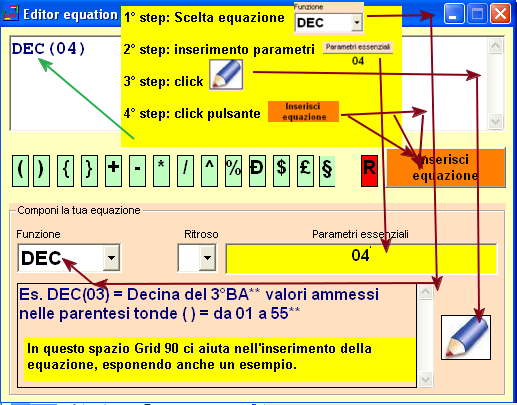
inserimento di una equazione:
Esempio di
inserimento di una equazione:
N.B. imparate ad avvicinare il mouse alle
icone: potrebbero consigliarvi qualcosa.
1° step: scelta della equazione dalla casella funzione (qui
otterremo suggerimenti a video);
2° step: scelta dei parametri essenziali;
3° step: click sulla icona Matita;
4° step: click sul pulsante "Inserisci equazione".

 Le funzioni: c'e'
solo da perdere la testa
Le funzioni: c'e'
solo da perdere la testa
![]() FUN_1 ** DEC**= Esempio DEC(03) =
Decina del 3°BA** valori ammessi nelle parentesi tonde ( ) = da 01 a 55
FUN_1 ** DEC**= Esempio DEC(03) =
Decina del 3°BA** valori ammessi nelle parentesi tonde ( ) = da 01 a 55
![]() FUN_2=**NUM** Esempio NUM(07)= 2° ESTRATTO DI CAGLIARI. Con 07 si indica la
posizione. Essa, infatti, è la settima casella nel quadro estrazionale e
corrisponde appunto al secondo numero estratto su CAGLIARI.** valori ammessi
nelle parentesi tonde ( ) = da 01 a 55**
FUN_2=**NUM** Esempio NUM(07)= 2° ESTRATTO DI CAGLIARI. Con 07 si indica la
posizione. Essa, infatti, è la settima casella nel quadro estrazionale e
corrisponde appunto al secondo numero estratto su CAGLIARI.** valori ammessi
nelle parentesi tonde ( ) = da 01 a 55**
![]() FUN_3=FIG** Esempio FIG(13)= FIGURA DEL 3° ESTRATTO FIRENZE**** valori ammessi
nelle parentesi tonde ( ) = da 01 a 55**
FUN_3=FIG** Esempio FIG(13)= FIGURA DEL 3° ESTRATTO FIRENZE**** valori ammessi
nelle parentesi tonde ( ) = da 01 a 55**
![]() FUN_4=CAD**
Esempio CAD(54) = CADENZA DEL 4° ESTRATTO NAZIONALE** valori ammessi
nelle parentesi tonde ( ) = da 01 a 55**
FUN_4=CAD**
Esempio CAD(54) = CADENZA DEL 4° ESTRATTO NAZIONALE** valori ammessi
nelle parentesi tonde ( ) = da 01 a 55**
![]() FUN_5=SQR** Esempio SQR(55) = RADICE QUADRATA DEL 5° ESTRATTO NZ** valori ammessi
nelle parentesi tonde ( ) = da 01 a 55**
FUN_5=SQR** Esempio SQR(55) = RADICE QUADRATA DEL 5° ESTRATTO NZ** valori ammessi
nelle parentesi tonde ( ) = da 01 a 55**
FUN_6=VER** Esempio VER(55) = VERTIBILE DEL 5° ESTRATTO NAZIONALE** valori
ammessi nelle parentesi tonde ( ) = da 01 a 55**
![]() FUN_7=DDE** Esempio DDE(55) = DIAMETRALE DECINA DEL 5° NZ** valori ammessi nelle
parentesi tonde ( ) = da 01 a 55**
FUN_7=DDE** Esempio DDE(55) = DIAMETRALE DECINA DEL 5° NZ** valori ammessi nelle
parentesi tonde ( ) = da 01 a 55**
Non abbiate timore qualora il risultato restituisse zero virgola qualcosa, in quanto i valori Pmin e Pmax accettano anche lo "zero presenze", lo "zero punteggio", la "soluzione zero" .
Un esempio. Consideriamo l'estrazione dell'11 febbraio 2010. Il 4° Naz = 9 . Il suo diametrale in decina = 4. Il 5° estratto Naz = 50. Il suo diametrale in decina = 55. Eseguendo la divisione 4: 55= 0,072. Siccome la funzione prende solo la parte intera, allora il risultato della equazione sarà pari a zero. Possiamo catturare una spia del genere? Certo che sì. Ecco lo screenshot.
![]() FUN_8=DIA** Esempio DIA(55) = DIAMETRALE DEL 5° NZ** valori ammessi nelle
parentesi tonde ( ) = da 01 a 55**
FUN_8=DIA** Esempio DIA(55) = DIAMETRALE DEL 5° NZ** valori ammessi nelle
parentesi tonde ( ) = da 01 a 55**
![]() FUN_9=S91**Esempio S91(55) = SIMMETRICO A 91 DEL 5° NZ** valori ammessi nelle
parentesi tonde ( ) = da 01 a 55**
FUN_9=S91**Esempio S91(55) = SIMMETRICO A 91 DEL 5° NZ** valori ammessi nelle
parentesi tonde ( ) = da 01 a 55**
![]() FUN_10=C90** Esempio C90(55) = COMPLEMENTO A 90 DEL 5° NZ** valori ammessi nelle
parentesi tonde ( ) = da 01 a 55**
FUN_10=C90** Esempio C90(55) = COMPLEMENTO A 90 DEL 5° NZ** valori ammessi nelle
parentesi tonde ( ) = da 01 a 55**
![]() FUN_11=DIS** Esempio DIS(01.05) = DISTANZA FRA 1°BA e 5°BA** valori ammessi nelle
parentesi tonde ( ) = da 01 a 55**
FUN_11=DIS** Esempio DIS(01.05) = DISTANZA FRA 1°BA e 5°BA** valori ammessi nelle
parentesi tonde ( ) = da 01 a 55**
![]() FUN_12=DIF** Esempio DIF(21.25) = DIFFERENZA ASSOLUTA fra 1°MILANO e 5°MILANO**
valori ammessi nelle parentesi tonde ( ) = da 01 a 55**
FUN_12=DIF** Esempio DIF(21.25) = DIFFERENZA ASSOLUTA fra 1°MILANO e 5°MILANO**
valori ammessi nelle parentesi tonde ( ) = da 01 a 55**
![]() FUN_13=UNI** Esempio UNICD(01.55) = UNIONE della Cadenza 1°BA e Decina 5°NZ,
oppure UNIYW(02.53) = UNIONE fra il complemento90 del 2°BA ed il diametrale
del 3°NZ. Le due lettere finali indicano, quindi, cosa UNIRE. C=Cadenza,
D=Decina, F=Figura, V=Vertibile, Y=Complemento90, S=Simmetrico91,
W=Diametrale, J=Diametrale in decina** valori ammessi nelle parentesi tonde ( )
= da 01 a 55**
FUN_13=UNI** Esempio UNICD(01.55) = UNIONE della Cadenza 1°BA e Decina 5°NZ,
oppure UNIYW(02.53) = UNIONE fra il complemento90 del 2°BA ed il diametrale
del 3°NZ. Le due lettere finali indicano, quindi, cosa UNIRE. C=Cadenza,
D=Decina, F=Figura, V=Vertibile, Y=Complemento90, S=Simmetrico91,
W=Diametrale, J=Diametrale in decina** valori ammessi nelle parentesi tonde ( )
= da 01 a 55**
Tramite questa funzione potremo effettuare ogni tipo di unione possibile fra estratti del quadro estrazionale, sia con riferimento alla estrazione di attualità, sia con riferimento a 1,2,3 etc concorsi orsono.
La funzione è UNI, che significa unione. Ad essa affiancheremo coppie di lettere scelte nella casella V V. Ad ogni coppia di lettere contenute nella colonna V V corrispondono delle configurazioni assumibili di numeri e cioè:
C= CADENZA**F=FIGURA*D= DECINA**Y=COMPLEMENTO A 90**S= SIMMETRICO A 91**J= DIAMETRALE IN DECINA**W= DIAMETRALE**N= Numero fisso. Esempio UNIDN(55.18) = FAI UNIONE DELLA Decina del 5°Naz col fisso N 18**E = Estratto. Esempio UNIDE (55.18) = FAI UNIONE DELLA Decina del 5°Naz con l'estratto in posizione 18-esima.
![]() FUN_14=LUN** Esempio LUN09{1}(01.78.89) = prende la lunghetta FISSI 01.78.89 su
Torino (il valore dopo LUN può essere uno dei seguenti Ba = 01 ; Ca = 02, Fi
= 03; Ge = 04; Mi = 05; Na = 06; Pa = 07; Ro = 08; To = 09; Ve = 10; Naz =
11) di 1 concorso precedente e indica i punti realizzati.
FUN_14=LUN** Esempio LUN09{1}(01.78.89) = prende la lunghetta FISSI 01.78.89 su
Torino (il valore dopo LUN può essere uno dei seguenti Ba = 01 ; Ca = 02, Fi
= 03; Ge = 04; Mi = 05; Na = 06; Pa = 07; Ro = 08; To = 09; Ve = 10; Naz =
11) di 1 concorso precedente e indica i punti realizzati.
![]() FUN_15=LUX** Esempio LUX09{1}(01.02.55) = preleva le posizioni 1Ba, 2Ba e 5Nz su
Torino (il valore dopo LUX può essere uno dei seguenti Ba = 01 ; Ca = 02, Fi
= 03; Ge = 04; Mi = 05; Na = 06; Pa = 07; Ro = 08; To = 09; Ve = 10; Naz =
11) di 1 concorso fa e indica i punti totalizzati ** valori ammessi nelle
parentesi tonde ( ) = da 01 a 55**
FUN_15=LUX** Esempio LUX09{1}(01.02.55) = preleva le posizioni 1Ba, 2Ba e 5Nz su
Torino (il valore dopo LUX può essere uno dei seguenti Ba = 01 ; Ca = 02, Fi
= 03; Ge = 04; Mi = 05; Na = 06; Pa = 07; Ro = 08; To = 09; Ve = 10; Naz =
11) di 1 concorso fa e indica i punti totalizzati ** valori ammessi nelle
parentesi tonde ( ) = da 01 a 55**
![]() FUN_16=LUV** Esempio LUV09{1}(01.02.55) = preleva le posizioni 1Ba, 2Ba e 5Nz su
Torino (il valore dopo LUV può essere uno dei seguenti Ba = 01 ; Ca = 02, Fi
= 03; Ge = 04; Mi = 05; Na = 06; Pa = 07; Ro = 08; To = 09; Ve = 10; Naz =
11) di 1 concorso fa e le confronta con quelle di Torino del concorso
attuale** valori ammessi nelle parentesi tonde ( ) = da 01 a 55**
FUN_16=LUV** Esempio LUV09{1}(01.02.55) = preleva le posizioni 1Ba, 2Ba e 5Nz su
Torino (il valore dopo LUV può essere uno dei seguenti Ba = 01 ; Ca = 02, Fi
= 03; Ge = 04; Mi = 05; Na = 06; Pa = 07; Ro = 08; To = 09; Ve = 10; Naz =
11) di 1 concorso fa e le confronta con quelle di Torino del concorso
attuale** valori ammessi nelle parentesi tonde ( ) = da 01 a 55**
![]() FUN_17=SOM** Esempio SOM09{1}(85.44.23) = prende le 10 somme su Torino (il valore
dopo SOM può essere uno dei seguenti Ba = 01 ; Ca = 02, Fi = 03; Ge = 04; Mi
= 05; Na = 06; Pa = 07; Ro = 08; To = 09; Ve = 10; Naz = 11) di 1 concorso
fa e le confronta con le somme 85.44.23
FUN_17=SOM** Esempio SOM09{1}(85.44.23) = prende le 10 somme su Torino (il valore
dopo SOM può essere uno dei seguenti Ba = 01 ; Ca = 02, Fi = 03; Ge = 04; Mi
= 05; Na = 06; Pa = 07; Ro = 08; To = 09; Ve = 10; Naz = 11) di 1 concorso
fa e le confronta con le somme 85.44.23
![]() FUN_18=DSV** Esempio DSV09{1}(85.44.23) = prende le 10 distanze su Torino (il
valore dopo DSV può essere uno dei seguenti Ba = 01 ; Ca = 02, Fi = 03; Ge =
04; Mi = 05; Na = 06; Pa = 07; Ro = 08; To = 09; Ve = 10; Naz = 11) di 1
concorso fa e le confronta con le distanze 85.44.23.
FUN_18=DSV** Esempio DSV09{1}(85.44.23) = prende le 10 distanze su Torino (il
valore dopo DSV può essere uno dei seguenti Ba = 01 ; Ca = 02, Fi = 03; Ge =
04; Mi = 05; Na = 06; Pa = 07; Ro = 08; To = 09; Ve = 10; Naz = 11) di 1
concorso fa e le confronta con le distanze 85.44.23.
Questa funzione è simile alla precedente perchè permette di verificare se ci
sia eguaglianza fra un valore distanza da noi indicato rispetto alle 10
distanze che ad ogni estrazione si formano su ciascuna ruota. E' evidente
che la verifica potremo farla con riferimento all'estrazione di attualità,
oppure puntando sempre su 1, 2, 3...estrazioni a ritroso.
![]() FUN_19=DSI** Esempio DSI{1}(01.02.11) = prende le ruote Ba.Ca.Nz a due a due di 1
concorso fa e indica quante coppie di ruote hanno distanze ISOTOPE
svincolate** valori ammessi nelle parentesi tonde ( ) = da 01 a 11**
FUN_19=DSI** Esempio DSI{1}(01.02.11) = prende le ruote Ba.Ca.Nz a due a due di 1
concorso fa e indica quante coppie di ruote hanno distanze ISOTOPE
svincolate** valori ammessi nelle parentesi tonde ( ) = da 01 a 11**
Esempio: Consideriamo l'estrazione del 9 febbraio 2010
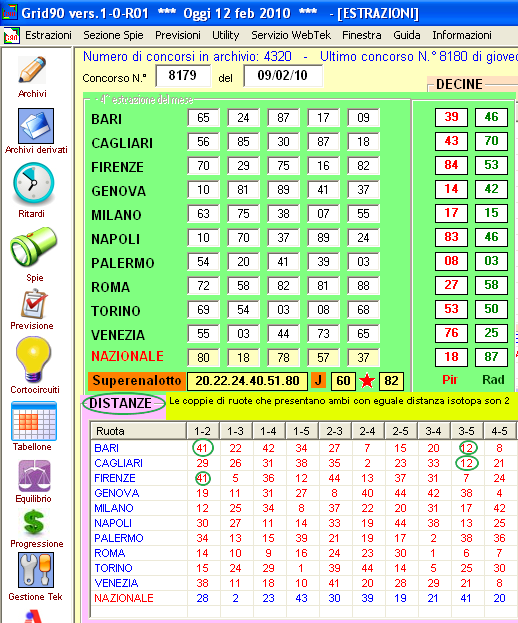
Qualora andassimo ad inserire nel tester l'equazione:
![]() FUN_20=SOI** Esempio SOI{1}(01.02.11) = prende le ruote Ba.Ca.Nz a due a due di 1
concorso fa e indica quante coppie di ruote hanno somme ISOTOPE svincolate**
valori ammessi nelle parentesi tonde ( ) = da 01 a 11**
FUN_20=SOI** Esempio SOI{1}(01.02.11) = prende le ruote Ba.Ca.Nz a due a due di 1
concorso fa e indica quante coppie di ruote hanno somme ISOTOPE svincolate**
valori ammessi nelle parentesi tonde ( ) = da 01 a 11**
![]() FUN_21=ACO** Esempio ACO{1}(01.02.11) = prende le ruote Ba.Ca.Nz a due a due di 1
concorso fa e indica quante coppie di ruote hanno come minimo l'ambo in
comune** valori ammessi nelle parentesi tonde ( ) = da 01 a 11**
FUN_21=ACO** Esempio ACO{1}(01.02.11) = prende le ruote Ba.Ca.Nz a due a due di 1
concorso fa e indica quante coppie di ruote hanno come minimo l'ambo in
comune** valori ammessi nelle parentesi tonde ( ) = da 01 a 11**
![]() FUN_22=AIS** Esempio AIS{1}(01.02.11) = prende le ruote Ba.Ca.Nz a due a due di 1
concorso fa e indica quante coppie di ruote hanno ambi isotopi in comune**
valori ammessi nelle parentesi tonde ( ) = da 01 a 11**
FUN_22=AIS** Esempio AIS{1}(01.02.11) = prende le ruote Ba.Ca.Nz a due a due di 1
concorso fa e indica quante coppie di ruote hanno ambi isotopi in comune**
valori ammessi nelle parentesi tonde ( ) = da 01 a 11**
![]() FUN_23= CLU** Esempio CLU21{1}(18.20.89) = analizza la terzina fissa 18.20.89 (ma
anche lunghette maggiori) e indica quante coppie di ruote presentano almeno
2 punti su ruota A e 1 punto su ruota B o viceversa.
FUN_23= CLU** Esempio CLU21{1}(18.20.89) = analizza la terzina fissa 18.20.89 (ma
anche lunghette maggiori) e indica quante coppie di ruote presentano almeno
2 punti su ruota A e 1 punto su ruota B o viceversa.
![]() FUN_24=SUM** Esempio SUM(01.05) = SOMMA 1°BA e 5°BA e procede, eventualmente, a
fare il fuori 90.** valori ammessi nelle parentesi tonde ( ) = da 01 a 55**.
Molto semplice questa funzione.
FUN_24=SUM** Esempio SUM(01.05) = SOMMA 1°BA e 5°BA e procede, eventualmente, a
fare il fuori 90.** valori ammessi nelle parentesi tonde ( ) = da 01 a 55**.
Molto semplice questa funzione.
![]() FUN_25=ATR** Esempio ATR(01.05.55) = Calcola area del TRIANGOLO che si forma
disponendo sul cerchio ciclometrico il valore del 1°BA, 5°BA e 5°NZ.
Il
valore max che può assumere l'area del triangolo è 300( valore massimo
inseribile nella casella PMax).
FUN_25=ATR** Esempio ATR(01.05.55) = Calcola area del TRIANGOLO che si forma
disponendo sul cerchio ciclometrico il valore del 1°BA, 5°BA e 5°NZ.
Il
valore max che può assumere l'area del triangolo è 300( valore massimo
inseribile nella casella PMax).
Nel caso di terzine
simmetriche, come ad esempio la 30.60.90, L'AREA DEL TRIANGOLO sarà : A x B x C /
4r(90). Utilizzando ATR(01.05.55)+ ATR(01.06.55) SI OTTERRA' L'AREA DEL
QUADRILATERO.
UTILIZZANDO IL TRIPLO ATR SI OTTERRA' L'AREA DEI POLIGONI.
![]() FUN_26=RAD** Esempio RAD{2}(09) = Calcola la RADICE QUADRATA del numero composto
dai 5 estratti sulla ruota di TORINO di 2 concorsi precedenti. La ruota 01 è
BARI, la 02 CAGLIARI e così via fino alla 11 che è la ruota NAZIONALE. I
concorsi a ritroso esaminabili sono max 9 e tale parametro è opzionale.
FUN_26=RAD** Esempio RAD{2}(09) = Calcola la RADICE QUADRATA del numero composto
dai 5 estratti sulla ruota di TORINO di 2 concorsi precedenti. La ruota 01 è
BARI, la 02 CAGLIARI e così via fino alla 11 che è la ruota NAZIONALE. I
concorsi a ritroso esaminabili sono max 9 e tale parametro è opzionale.
Quando avvertiamo la necessità di catturare spie basate su un determinato
valore della radice quadrata dei numeri di una ruota specifica, useremo tale
funzione la quale ci permette di eseguire calcoli non solo sull'estrazione
attuale quanto anche su quelle a ritroso.
![]() FUN_27=PIR** Esempio PIR{9}(07) = Calcola la
PIRAMIDE del numero formato dai 5 estratti sulla ruota di PALERMO
**Notazione (07)** di 9 concorsi precedenti **Notazione {9}**. La ruota 01 è
BARI, la 02 CAGLIARI e così via fino alla 11 che è la ruota NAZIONALE
(Trattasi dei valori inclusi fra parentesi tonde).
I concorsi a ritroso esaminabili sono max 9 e tale
parametro è opzionale.
FUN_27=PIR** Esempio PIR{9}(07) = Calcola la
PIRAMIDE del numero formato dai 5 estratti sulla ruota di PALERMO
**Notazione (07)** di 9 concorsi precedenti **Notazione {9}**. La ruota 01 è
BARI, la 02 CAGLIARI e così via fino alla 11 che è la ruota NAZIONALE
(Trattasi dei valori inclusi fra parentesi tonde).
I concorsi a ritroso esaminabili sono max 9 e tale
parametro è opzionale.
![]() FUN_28=RIT**
Esempio RIT{3}(55) = Calcola il ritardo del 5° numero estratto sulla
ruota Nazionale** notazione (55)**,di tre concorsi prima **notazione
{3}***Il valore del ritardo viene misurato facendo riferimento a un attimo
prima della sua estrazione dall'urna. (Se nell'ultima estrazione sortisce il
25, il ritardo viene calcolato facendo riferimento al periodo che precede la
sua estrazione. I concorsi a ritroso esaminabili sono
max 9 e tale parametro è opzionale.
FUN_28=RIT**
Esempio RIT{3}(55) = Calcola il ritardo del 5° numero estratto sulla
ruota Nazionale** notazione (55)**,di tre concorsi prima **notazione
{3}***Il valore del ritardo viene misurato facendo riferimento a un attimo
prima della sua estrazione dall'urna. (Se nell'ultima estrazione sortisce il
25, il ritardo viene calcolato facendo riferimento al periodo che precede la
sua estrazione. I concorsi a ritroso esaminabili sono
max 9 e tale parametro è opzionale.
 Equazioni
speciali nidificate
Equazioni
speciali nidificate
Le equazioni NIDIFICATE sono davvero così
tante, miliardi, che esporle tutte sarebbe una improbabile impresa. Allora,
abbiamo pensato di presentare un excursus delle
F.N.M, funzioni nidificate master
evidenziando quelle equazioni che potrete usare come "sorgenti", come base.
Infatti, da esse ne potrete derivare così tante da impallidire: vi basterà
apportare leggere modifiche, lievi ristrutturazioni onde costituirvi una
base invidiabile di formule matematiche.
![]() Filtro Quantità Numeri netti
(Qt Num Netti)
Filtro Quantità Numeri netti
(Qt Num Netti)
In questo screenshot, tra l'altro, noterete la presenza di una casella gialla che accoglie i Numeri Residui Netti:
![]() Quindi, per ciascuna estrazione otterremo la visualizzazione dei numeri residui netti, al netto dei doppioni. I numeri residui netti sono variabili perchè non in ogni estrazione è dato riscontrare la stessa quantità di doppioni.
Quindi, per ciascuna estrazione otterremo la visualizzazione dei numeri residui netti, al netto dei doppioni. I numeri residui netti sono variabili perchè non in ogni estrazione è dato riscontrare la stessa quantità di doppioni.
![]() Come si inserisce la equazione Quantità Numeri netti
(Qt Num Netti)
Come si inserisce la equazione Quantità Numeri netti
(Qt Num Netti)
![]() Filtro Numeri residui netti
(Num residui)
Filtro Numeri residui netti
(Num residui)
![]() Filtro Posizione residui
(Posizione residui)
Filtro Posizione residui
(Posizione residui)
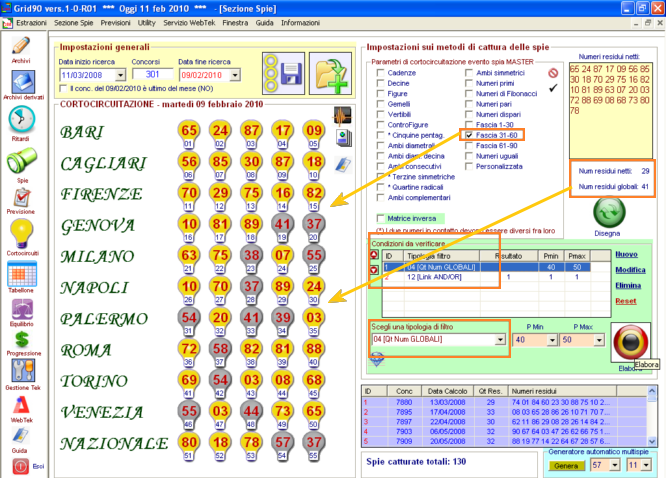
Per comprendere al meglio questo filtro è necessario diate uno sguardo attento allo screenshot esplicativo seguente:
Qualora avessimo imposto al controllo
Link And/Or come valori PMin e PMax 1 e 2, Grid 90 avrebbe catturato tutti quegli eventi in cui almeno una delle due posizioni, la prima o seconda, facessero riferimento a numeri accesi e quindi fossero presenti nella griglia gialla che accoglie i numeri residui.
 Filtro Quantità Numeri
Globali
(Qt Num GLOBALI)
Filtro Quantità Numeri
Globali
(Qt Num GLOBALI)
Sono necessarie
alcune considerazioni.
I numeri globali al massimo sono 55,
perché 55 sono gli estratti.
Questo è vero fino a che non introduciamo dei parametri che limitino tali
numeri.
Abbiamo visto che selezionando il parametro fascia
31-60 faremo spegnere nella estrazione a lato tutti
quei numeri dal 31 al 60.
Ne deriverà un quadro estrazionale ove saranno
accesi quei numeri diversi da quelli appartenenti al range
31.60.
Orbene, i numeri accesi nella loro totalità corrispondono ai
numeri residui globali,
mentre i
numeri residui netti
saranno equivalenti ai
numeri residui globali meno i doppioni.
Quindi i numeri globali possano essere anche di quantità inferiore a 55 ed è
legittima la cattura di quelle estrazioni ove i numeri globali residui abbiano
una valore compreso fra 40 a 50.
I filtri,
che m'appresso ad esporvi, sono quanto di più
avanzato possiate immaginare.
La motivazione risiede nella circostanza che è
permesso utilizzare più filtri nel medesimo step di cattura degli eventi spia,
tanto da abbracciare accadimenti estrazionali
che prima era solo una pia illusione il poterli intercettare.
Non pensiate di poter comprendere ogni cosa, poiché l'argomento è di una vastità
scevra da precedenti, ma l'apprendere le basi vi porterà a sconfinare su
territori distanti e vastissimi dei quali vi stupirà la bellezza, la potenza ...
e la sua proiezione al futuro.
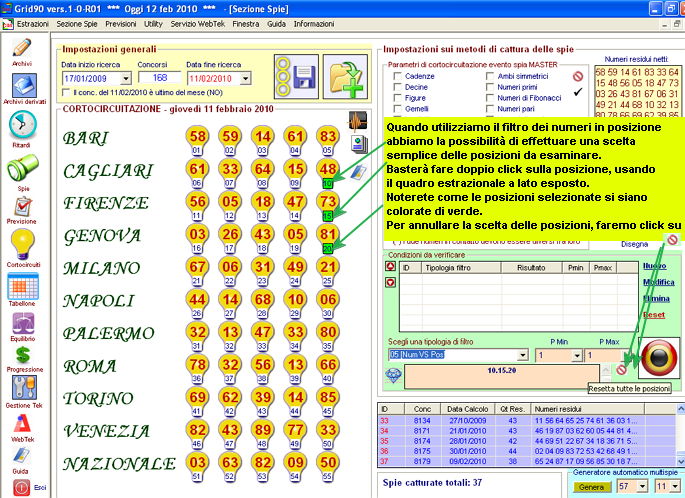
 Filtro Posizione
dei numeri
(Num VS Pos)
Filtro Posizione
dei numeri
(Num VS Pos)
![]() Filtro Estrazione
mensile
(Estraz. Mensile )
Filtro Estrazione
mensile
(Estraz. Mensile )
![]() Filtro
Arco Temporale
(Arco Temporale)
Filtro
Arco Temporale
(Arco Temporale)
![]() Filtro Giorni
Settimanali
(Giorni settimanali)
Filtro Giorni
Settimanali
(Giorni settimanali)
 Filtro Anni Pari e
Dispari
(Anni P/D)
Filtro Anni Pari e
Dispari
(Anni P/D)
 Filtro
Statistica Continua
(Statistica CONTINUA)
Filtro
Statistica Continua
(Statistica CONTINUA)
 La
circuitazione
La
circuitazione
In maniera più specifica si definisce "Circuitazione"
l'interconnessione di elementi numerici
uniti assieme da modelli matematici in un percorso chiuso.
Il percorso chiuso è rappresentato dal quadro
estrazionale. Esso è il circuito.
I modelli matematici sono rappresentati dai parametri limitativi,
come le cadenze,
le figure, le decine, gli ambi consecutivi, diametrali etc.
Questi elementi fanno accendere e spegnere i numeri del quadro
estrazionale.
Lo spegnimento dei numeri nel quadro estrazionale è garantito da un
legame di vicinanza, da un legame di adiacenza orizzontale, verticale e
diagonale dei numeri.
L'utilizzo dei parametri limitativi serve a ridurre la massa
estrazionale dei numeri residui globali e dei numeri residui netti. Questa
operazione assumerà importanza sia quando cattureremo l'evento spia, sia
quando lo importeremo nelle sezioni previsionali per la elaborazione degli
output.
Nella griglia
possiamo selezionare una o più caselle.
La selezione avviene checkando, mettendo il segno di spunta accanto alla
voce interessata.
Ad esempio, selezionando la casella Fascia 31- 60 e CLICCANDO SULLA
ICONA "DISEGNA" faremo spegnere nel quadro estrazionale quei numeri che
rientrino in codesta fascia e che siano in contatto fra di loro (adiacenti). Lo spegnimento è
però una operazione particolare poiché avviene solo per quei numeri che
siano vicini orizzontalmente, o verticalmente o diagonalmente.
Ecco la schermata:

![]() Una
volta che alcuni numeri risulteranno spenti, quelli accesi andranno a
costituire la Massa dei Numeri residui Globali. Eliminando da questi i
doppioni, otterremo i Numeri residui Netti che verranno utilizzati nelle
diverse sezioni previsionali: essi rappresenteranno
la base per la elaborazione di strepitosi modelli previsionali. Ve ne
renderete conto nel momento opportuno.
Una
volta che alcuni numeri risulteranno spenti, quelli accesi andranno a
costituire la Massa dei Numeri residui Globali. Eliminando da questi i
doppioni, otterremo i Numeri residui Netti che verranno utilizzati nelle
diverse sezioni previsionali: essi rappresenteranno
la base per la elaborazione di strepitosi modelli previsionali. Ve ne
renderete conto nel momento opportuno.
La griglia dei parametri limitativi, che ripetiamo
essere elementi di spegnimento e accensione dei numeri
presenti nel quadro estrazionale, sono rappresentati da configurazioni
numeriche che conosciamo sicuramente: le cadenze,
le decine, le figure, le
terzine simmetriche, come 30.60.90, oppure
31.61.01 etc;
i numeri pari e i numeri dispari; gli ambi diametrali
cioè quelli con distanza 45; gli ambi simmetrici , cioè quelli di
somma pari a 91;
gli ambi vertibili, gli ambi complementari cioè
quelli di somma 90 etc.
Per alcuni di essi forse non avrete piena cognizione, ragione per la quale
è d'uopo spiegarne la composizione.
 Cinquine
pentagonali
Cinquine
pentagonali
Questo termine viene riferito ad una
serie di 5 numeri la cui distanza è pari a 18 unità (ad esempio 1-19-37-55-73).
Con i 90 numeri sono possibili 18 serie diverse.
| 1 19 37 55 73 | 10 28 46 64 82 |
| 2 20 38 56 74 | 11 29 47 65 83 |
| 3 21 39 57 75 | 12 30 48 66 84 |
| 4 22 40 58 76 | 13 31 49 67 85 |
| 5 23 41 59 77 | 14 32 50 68 86 |
| 6 24 42 60 78 | 15 33 51 69 87 |
| 7 25 43 61 79 | 16 34 52 70 88 |
| 8 26 44 62 80 | 17 35 53 71 89 |
| 9 27 45 63 81 | 18 36 54 72 90 |
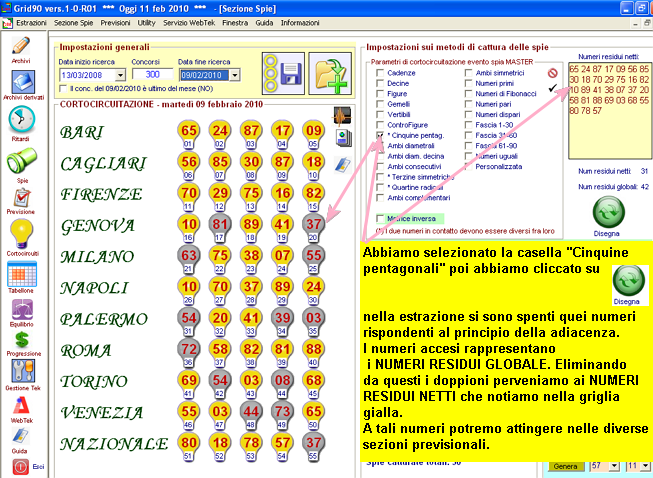
![]() I numeri di Fibonacci
I numeri di Fibonacci
La Serie di Fibonacci è una particolare sequenza di numeri la cui caratteristica principale è che ogni numero è dato dalla somma dei due valori che lo precedono. I numeri della sequenza sono infiniti, ma per ovvie ragioni quelli applicabili al gioco del lotto sono 10:
![]() 1, 2, 3, 5, 8, 13, 21, 34, 55, 89.
1, 2, 3, 5, 8, 13, 21, 34, 55, 89.
Se proviamo a selezionare la check box dei numeri di Fibonacci otterremo lo spegnimento nella griglia estrazione di quei numeri facenti parte della serie e che siano in contatto fra di loro.
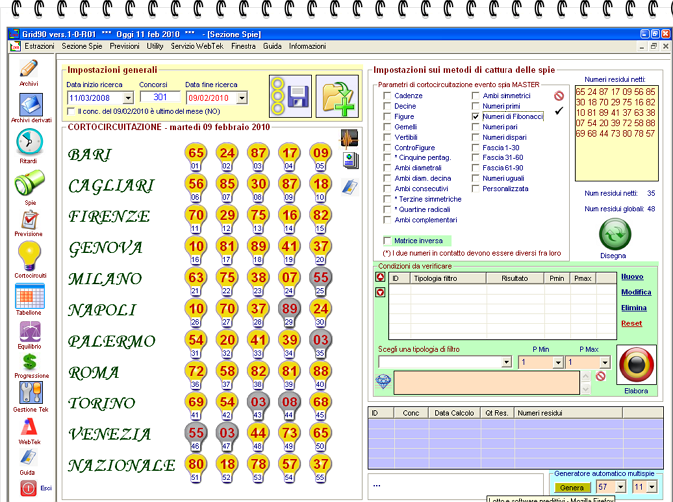
![]() Le controfigure
Le controfigure
Sono 10 gruppi formati da 9 numeri la cui distanza è sempre pari a 11. La controfigura 2 è la seguente: 2-13-24-35-46-57-68-79-90.
A partire dalla terza controfigura viene considerato, nella tabella seguente, come ultimo del gruppo , il gemello corrispondente al numero naturale.
Pertanto il n. 91 è sostituito dall'11, il 92 dal 22 e così via.
| Controfigura 1 | 1 12 23 34 45 56 67 78 89 |
| Controfigura 2 | 2 13 24 35 46 57 68 79 90 |
| Controfigura 3 | 3 14 25 36 47 58 69 80 11 |
| Controfigura 4 | 4 15 26 37 48 59 70 81 22 |
| Controfigura 5 | 5 16 27 37 49 60 71 82 33 |
| Controfigura 6 | 6 17 28 39 50 61 72 83 44 |
| Controfigura 7 | 7 18 29 40 51 62 73 84 55 |
| Controfigura 8 | 8 19 30 41 52 63 74 85 66 |
| Controfigura 9 | 9 20 31 42 53 64 75 86 77 |
| Controfigura 10 | 10 21 32 43 54 65 76 87 88 |
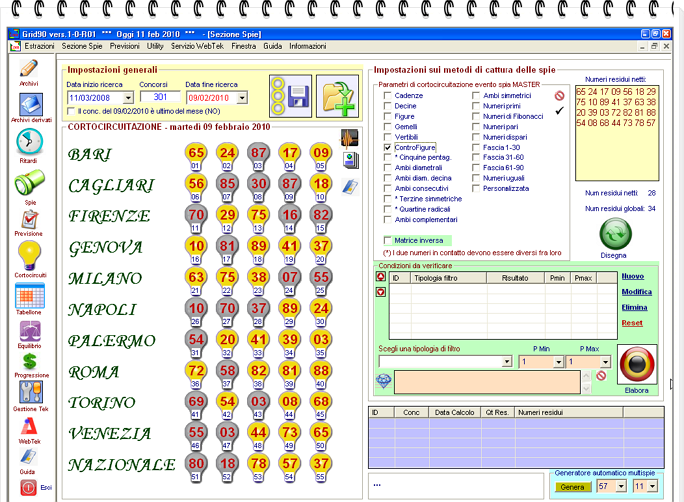
![]() I Numeri Primi
I Numeri Primi
Ecco la serie dei numeri primi: 2-3-5-7-11-13-17-19-23-29-31-37-41-43-47-53-59-61-67-71-73-79-83-89
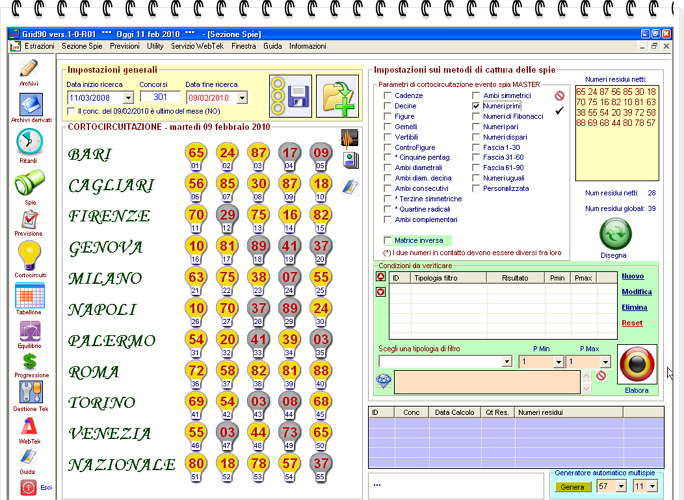
![]() La personalizzata
La personalizzata
Notiamo tra i parametri di cortocircuitazione due caselle interessanti: la casella Matrice Inversa e la casella Personalizzata.
Cliccando sulla casella personalizzata avremo modo di inserire numeri personali da noi preferiti e utilizzarli come elementi di spegnimento dei valori estrazionali. La casella personalizzata funge da elemento di completamento poiché rende possibile creare serie numeriche alle quali applicare il principio del circuito. Inserendo, ad esempio, 13.14.15 e cliccando sul pulsante "Disegna" potrei verificare l'effetto prodotto sul quadro estrazionale e come derivazione sui numeri residui.
La funzione della personalizzata agisce in duplice maniera: possiamo inserire numeri a scelti e verificare l'impatto sul quadro estrazionale, rispettando il principio di circuitazione, oppure possiamo considerare l'impatto sul quadro estrazionale senza legami di circuitazione, senza che vi sia la necessità che i numeri indicati rispondano al principio del contatto.
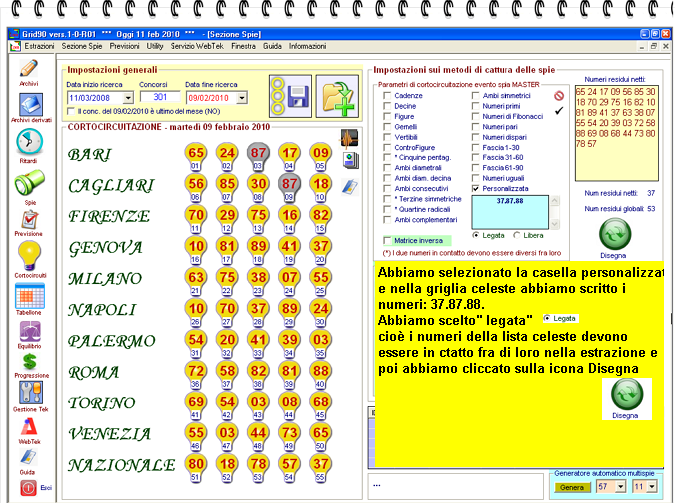
Qualora, anziché legata, avessimo scelto la circuitazione libera, cioè senza esigere che i numeri della lista personalizzata fossero in contatto nella estrazione, avremmo ottenuto una situazione di questo genere:
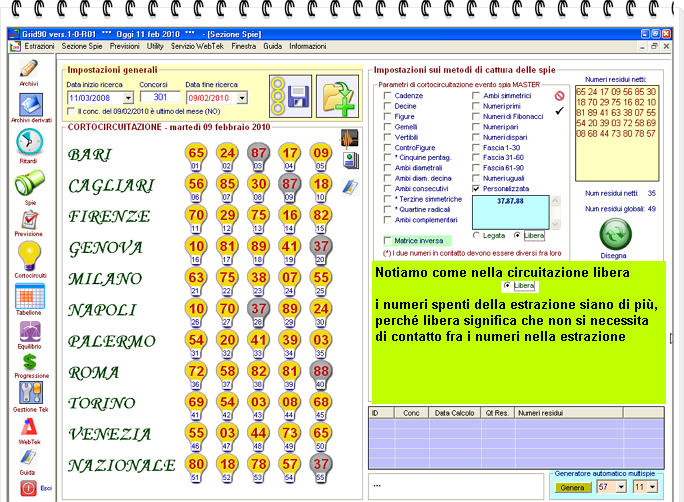
La matrice inversa
La casella inerente la matrice inversa presuppone che sia stata checkata, selezionata almeno un'altra casella dei parametri di limitazione. In breve: si selezionano i numeri di Fibonacci ... e la matrice inversa; si selezionano i numeri primi ... e la matrice inversa; si seleziona qualunque altro parametro numerico e ... la matrice inversa:
La matrice inversa cattura come numeri residui esattamente quelli esclusi tramite l'utilizzo di uno dei parametri. Ad esempio, la matrice inversa dei numeri primi equivale ai numeri primi stessi. Infatti, se checkassimo solo la casella numeri primi e pigiassimo sulla icona "Disegna", nella griglia estrazionale verrebbero spenti i numeri primi con la conseguenza che i numeri residui andrebbero a contenere solo i numeri residuanti della griglia estrazionale.
Selezionando, invece, la matrice inversa i numeri residui andrebbero a contenere esattamente i valori esclusi dalla griglia estrazionale e corrispondenti ai numeri primi stessi.
Vi mostro alcune schermate esaustive:
1° step: selezione Numeri di Fibonacci
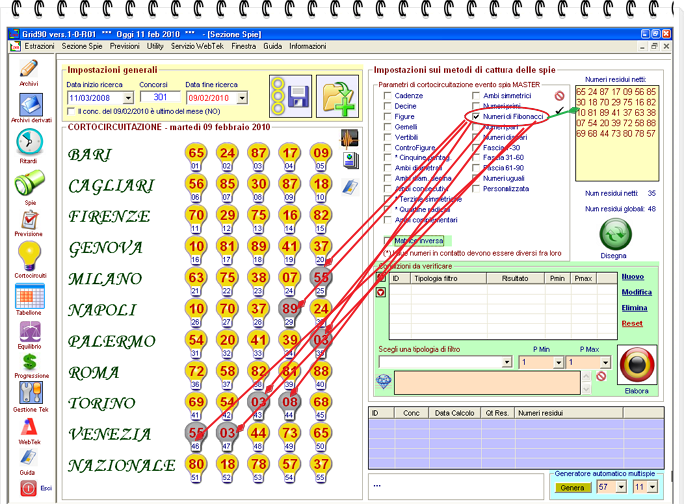
2° step: selezione della casellina "Matrice inversa"
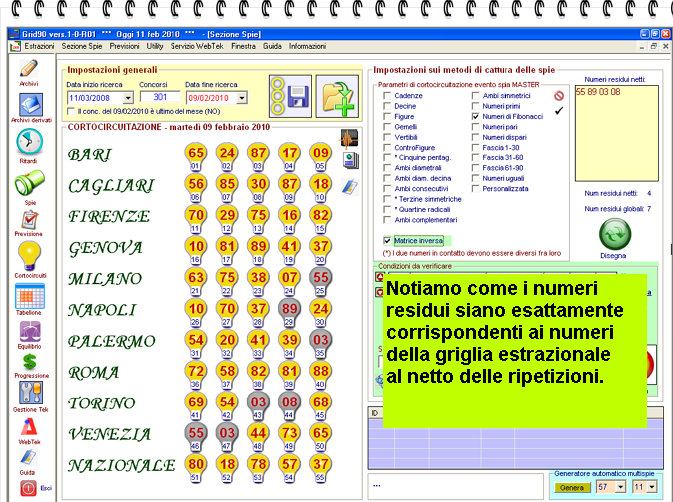
L'importanza di questa modalità risiede nella possibilità di catturare eventi spia come: la sortita di numeri appartenenti alle cinquine pentagonali in qualunque posizione; di numeri appartenenti agli ambi simmetrici in qualunque posizione.
Esempio: cattura ambi simmetrici:
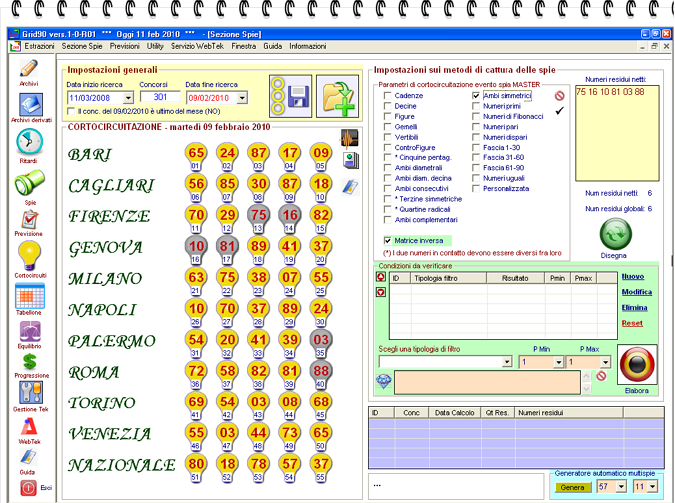
Esempio: cattura di un numero in qualunque posizione
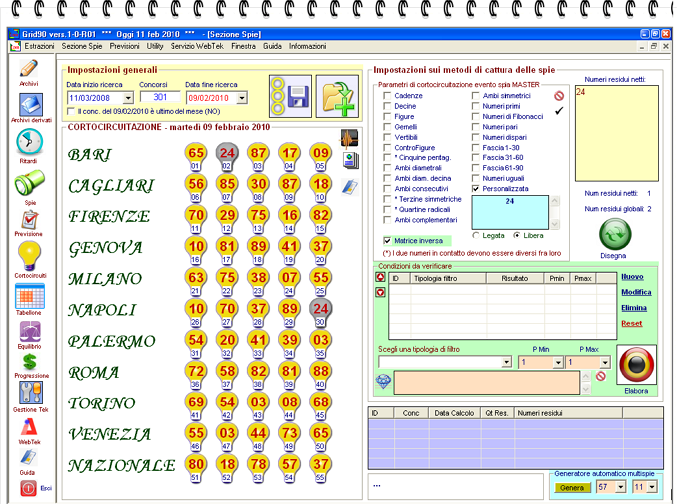
Vi immaginati i risvolti in termini di cattura di eventi spia, impossibili da intercettare con qualunque software?
No? ...peggio per
voi:-)
Clicca qui ritornare al menù principale
![]() Cliccare
sul pulsante next per andare avanti e back indietro ,nel tour guidato
Cliccare
sul pulsante next per andare avanti e back indietro ,nel tour guidato
![]()