PlugStat: le statistiche avanzate 
N.B. Obbligatoria la connessione internet attiva

Il plugin statistico di Vinco Premium Special è una assoluta innovazione nel campo dei modelli previsionali di natura stocastica. Esso tratta del principio dei Ritardi Areali ed espone una serie di valori, chiamati di condensazione, che si dipanano fra lo scarto quadratico medio, alla varianza, dal coefficiente di volatilità a l ritardo medio.

Alla routine si accede o dal menù in alto, oppure selezionando la icona esposta nella banda laterale denominata PlugStat.
 La routine è composta da:
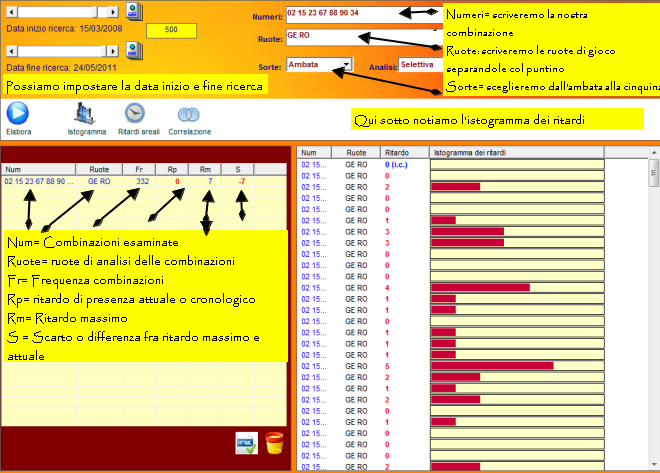
Data inizio e fine ricerca  
Una casella ove potremo scrivere il numero di concorsi da analizzare 
Una casella numeri ove scriveremo la combinazione da esaminare 
Una casella sorte ove scriveremo la sorte analizzata, dall'ambata alla cinquina 
Una casella ruote ove scriveremo le ruote di analisi separandole col puntino 
Una casella analisi che può essere "Selettiva", e in questo caso si esamina la combinazione da noi scritta nella casella "Numeri" e "Da file" che ci consente di scegliere uno dei tantissimi file cmb a disposizione da analizzare.

I ritardi areali e le statistiche avanzate
Tra due o più ritardi qualsiasi c'e' uno spazio, v'è una distanza. In geometria, lo spazio viene definito tramitel'area: essa rappresenta la misura dimensionale di una estensione qualsiasi. In geometria cartesiana, l'area viene misurata attraverso funzioni integrali. Tralasciando le modalità di calcolo, che rimangono ancorate ad un principio matematico-logico, la routine Stat di Vinco Premium Special espone diversi dati riferiti ai ritardi e, in modo particolare, i ritardi di area, o areali. Accanto a valori definiti tipici, come il ritardo di presenza attuale, cioè il ritardo cronologico sostanziale di una combinazione e il ritardo massimo nonché l'eventuale scarto differenziale e la FREQUENZA, e al di là del ritardo medio di una combinazione, troviamo il ritardo d'area attuale, quello massimo, il valore coassiale, lo scarto quadratico medio, la varianza e il coefficiente di volatilità.
Il ritardo di presenza attuale misura il numero di estrazioni, o concorsi, nei quali il numero, o quella combinazione, non è sortito, non è presente. Scelto un range estrazionale, data inizio e fine ricerca, oppure indicato un numero di estrazioni a piacere nell'apposita casellina, potremo analizzare numeri di nostro gradimento, oppure combinazioni presenti nel programma che vanno dai singoli numeri a tutti gli ambi, alle terzine,quartine, cinquine, novine, ottine, decine, ...trentine e per qualunque sorte, dall'ambata alla cinquina. La elaborazione ci fornirà il dato del ritardo di presenza, così come il ritardo massimo di quel numero o combinazione in quel range concorsuale. Già tali dati assumono ampia rilevanza ove si pensi che una delle tipiche scelte del giocatore è quella di considerare, come eventualità di gioco, le combinazioni il cui ritardo di presenta disti pochi concorsi da quello massimo. Altra modalità che appassiona il cultore è lo scarto (lettera S) tra il ritardo massimo e quello attuale. E' una indicazione che immediatamente fa emergere la distanza che intercorre fra le due forme di ritardo. 

Lo scarto quadratico medio dei ritardi
Lo scarto quadratico medio  (sca nella tabella) di una serie di ritardi è la media quadratica degli scarti dei singoli dati rispetto al ritardo medio. Tale indice indica la deviazione e la oscillazione della distribuzione dei ritardi. Essa cambia da ruota a ruota, e tenuto conto anche del range estrazionale di analisi. Basta eseguire una analisi sul medesimo compartimento per un numero di concorsi diversi, tipicamente successivi, e rendersi conto dello "scarto di attualità" del ritardo.

Facciamo un esempio

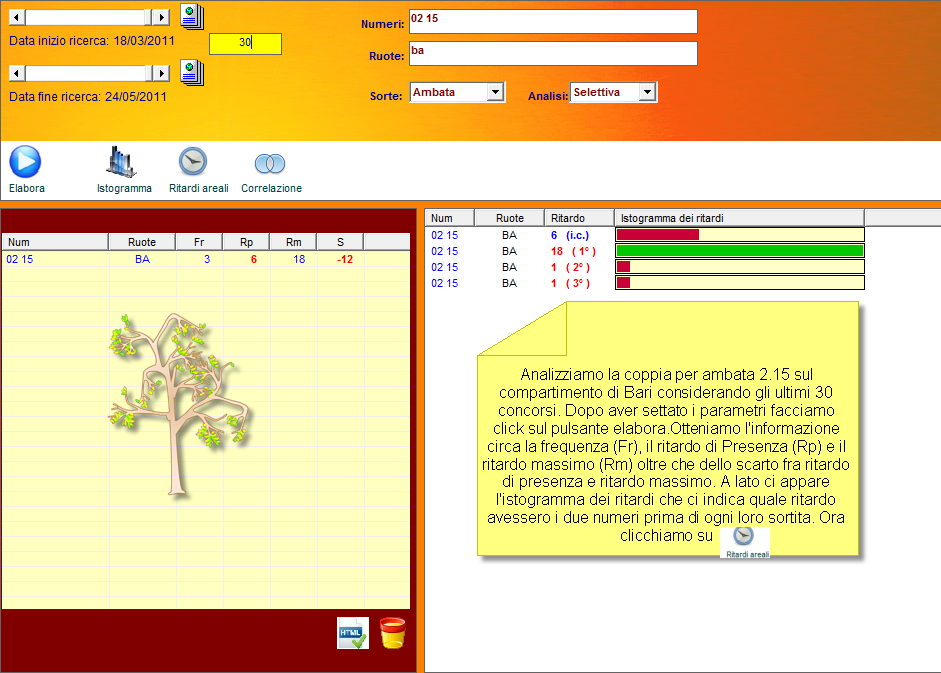
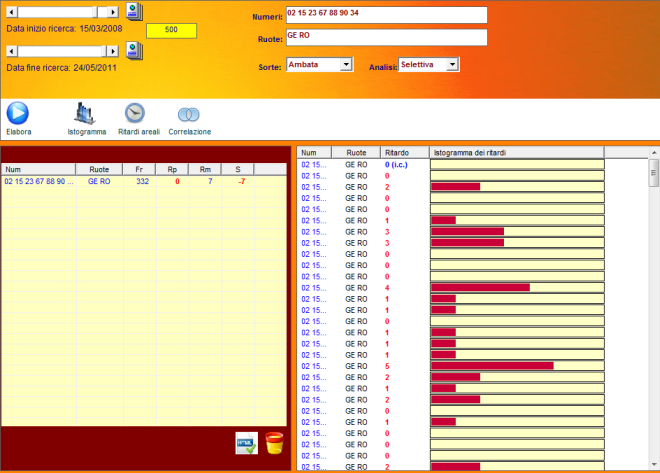
Clicchiamo su "Ritardi areali" e...

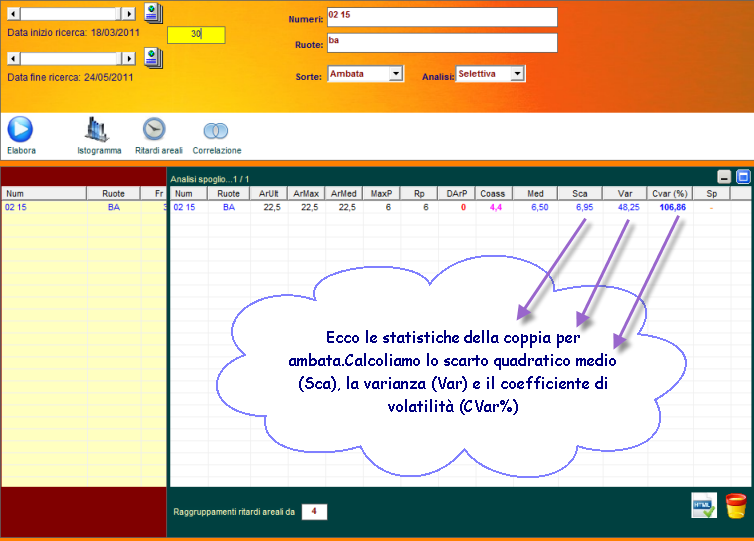
Per calcolare lo scarto quadratico dovremo prima computare la media dei ritardi. Essa si ottiene sommando i singoli ritardi e dividendo per il numero dei ritardi osservati. Nel nostro esempio: 
Quindi il ritardo medio, o media dei ritardi = 6,5. Applichiamo la formula per il calcolo dello scarto quadratico medio(colonna Sca) **radice quadrata di [(6-6,5)^2 + (18-6,5)^2 + (1-6,5)^2 + (1-6,5)^2]: 4 =6,95 (scarto quadratico medio). Nella formula 
M= ritardo medio = 6,5
x = i nostri 4 ritardi, cioè 6-18-1-1
n= numero ritardi osservati, cioè 4

Quanto più alto è il valore dello scarto quadratico medio tanto più alto è lo scostamento, la differenza fra il ritardo della combinazione alla sua sortita rispetto al ritardo medio. Nel nostro esempio il ritardo medio della combinazione è 6,5 concorsi (mediamente sortisce ogni 6,5 estrazioni). Lo scarto quadratico medio è 6,95 vicino al ritardo medio e quindi indica che le sortite, nel range estrazionale, mediamente si avvicinano al ritardo medio. 
Lo Scarto Quadratico Medio indica la variabilità rispetto alla media dei ritardi. Più il suo valore è alto, rispetto al ritardo medio, più è probabile che il trend futuro manifesterà ritardi consistenti o ritardi bassi rispetto al valore medio. Ad esempio, un valore alto dello scarto quadratico medio può essere dunque usato per una previsione sortita all'ultima estrazione, che presenti un basso ritardo medio e che che negli ultimi 2 o 3 casi ha presentato ritardi sopra il valore medio. 
Se il valore dello scarto si discosta dal valore del ritardo medio, è probabile che la combinazione in gioco mantenga un trend di sortite mediamente oscillanti rispetto al valore medio.

La varianza (Colonna Cvar%)

Per ottenere il valore di questo indice di dispersione basta moltiplicare per se stesso il valore dello scarto quadratico medio. Nel nostro esempio, lo scarto quadratico medio è pari a 6,95. Allora, 6,95 x 6,95 = 48 circa.

In teoria della probabilità e in statistica la varianza  è un numero che fornisce una misura di quanto siano vari i valori assunti dalla variabile, ovvero di quanto si discostino dalla media dei ritardi. La varianza ci fornisce una misura di come le sortite di una combinazione si posizionano attorno alla media. Questo dato è particolarmente interessante quando è necessario confrontare due combinazioni che hanno più o meno la stessa frequenza effettiva. In tal caso infatti andrà scelta la combinazione che ha varianza minore in quanto possiede una maggiore "regolarità", cioè quel numero che sortisce sempre con un livello di ritardo intorno alla media.

L'indice di volatilità (Colonna CVar%)

Se dobbiamo confrontare la variabilità dei ritardi in % si ricorre al coefficiente di variazione o volatilità o dispersione (CVar%).
Esso si ottiene nel modo seguente: (100 x Scarto quadratico medio):ritardo medio, Solitamente, quanto più basso è tale valore, tanto più alta è la probabilità di sortita di quella combinazione per la sorte analizzata. L'indice palesa se quella combinazione disperde le sue sortite distanziandosi poco, abbastanza o molto rispetto al ritardo medio.

L'indice DArP

Esso rappresenta la distanza fra il ritardo areale massimo previsto per una combinazione, colonna MaxP,  rispetto al ritardo di presenza attuale, colonna RP. Il ritardo areale massimo è ben differente dal ritardo massimo di una combinazione. Quest'ultimo è un dato conosciuto, mentre il ritardo max areale è un dato previsionato, valutato, predetto tenuto conto dei diversi valori areali di ritardo. Tale valore è un indicatore oltre al quale un ritardo areale non dovrebbe andare.

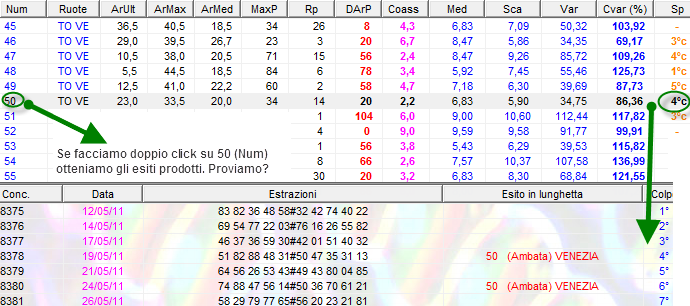
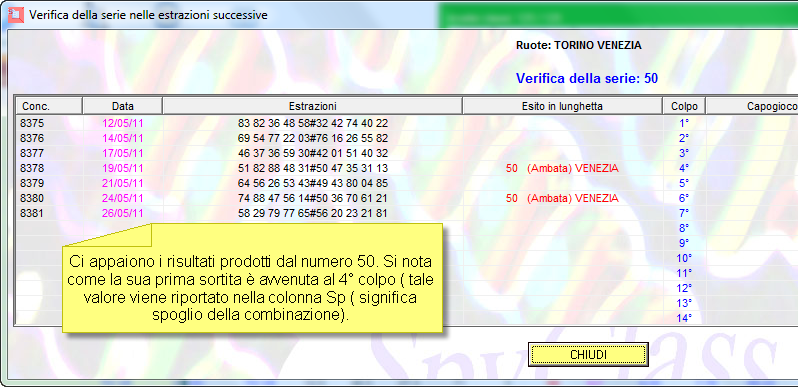
La colonna SP e il doppio click sul numero in previsione.

La colonna Sp è l'ultima visualizzata nella griglia dei ritardi areali. Essa significa "Spoglio combinazione". Quando è valorizzata ci indica il colpo di esito della combinazione che troviamo nella prima colonna della griglia dei ritardi areali. Se facciamo doppio click sulla combinazione verifichiamo gli esiti da essa prodotti.

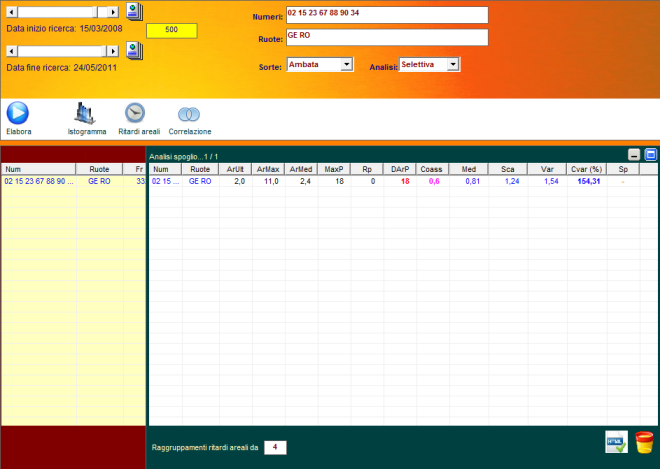
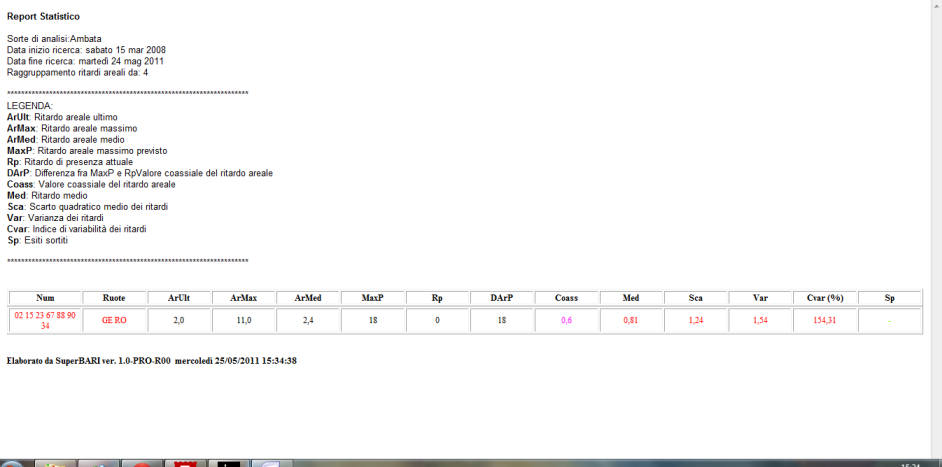
Le colonne ArUlt, ArMax, ArMed

La colonna AeUlt indica il ritardo areale ultimo, la colonna ArMax indica il ritardo areale Massimo e la colonna ArMed indica il ritardo areale medio. Trattasi di ritardi assolutamente diversi da quelli finora conosciuti e che pure vengono rappresentati nel PlugStat, come il ritardo attuale di presenza, il ritardo massimo.
I ritardi areali sono ulteriori misure di valutazione della maturazione per la sortita di una combinazione. Attraverso questi 3 indici sarà possibile inquadrare un modello previsionale verificando soprattutto quei valori il cui ritardo areale attuale sia adiacente al ritardo areale medio. Quando ci troviamo di fronte ad una combinazione che presenti un ritardo attuale areale vicino a quello medio, potrebbe essere opportuno porla in gioco.

Considerazione qualitative

Sebbene il lotto rimanga un gioco aleatorio, l'utilizzo di statistiche profonde permette al cultore di ridurre la distanza esistente fra la probabilità e la certezza. Qualora giocassimo a casaccio per un tempo consistente, e nel tempo successivo puntassimo in base ad un modello previsionale matematico statistico, nel secondo caso otterremmo maggiori successi rispetto al primo. Ciò significa che lo studio delle oscillazioni alle quali i numeri sono soggetti porta a risultati di prestigio e, nella peggiore delle ipotesi, a ridurre al minimo le perdite.
I modelli previsionali possibili utilizzando il PlugStat di Vinco Premium Special sono straordinariamente numerosi, così come alcuni strepitosamente vincenti. Ma come si crea il modello previsionale? Esso dovrà basarsi sulla osservazione del comportamento dei numeri in cicli estrazionali omogenei per numero di concorsi. Ad esempio, possiamo valutare l'impatto degli indici statistici in 3 cicli di 180 estrazioni e verificare il range entro i quali gli stessi sono contenuti. Intercettare un andamento, nel breve periodo, rispettoso degli indici statistici, ci permetterà agevolmente d'incappare in vittorie "nutrientissime".

UTILIZZO DELL'INDICE C/VAR% COME MODELLO PREVISIONALE
Poniamoci 9/10 estrazioni addietro rispetto alla data di fine ricerca ed eseguiamo una analisi per 180 concorsi  utilizzando il file contenente i 90 numeri singoli, per la sorte di ambata su ruote diametrali (Bari-Napoli)

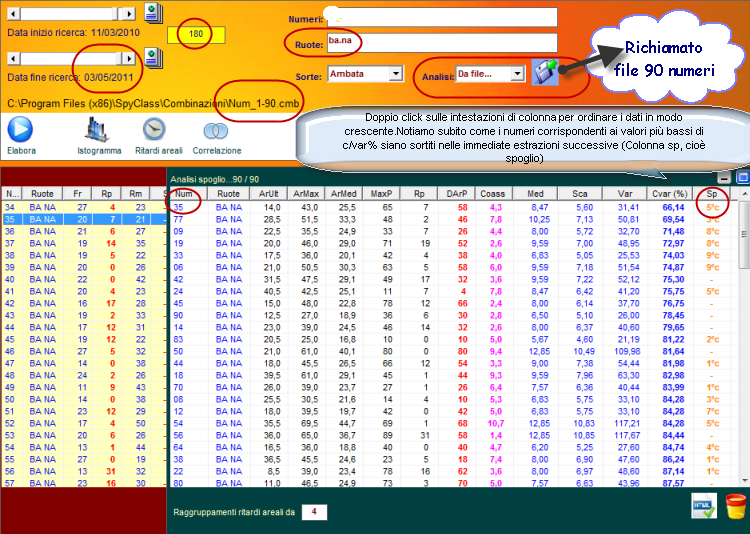
Notiamo come dopo aver ordinato in modo crescente la colonna CVar%, coefficiente di volatilità, i valori più bassi abbiano fornito l'esito fausto in pochi colpi di gioco. Siffatta analisi è possibile ripeterla anche per altri periodi estrazionali, onde verificare la bontà del modello previsionale visuale definito or ora.

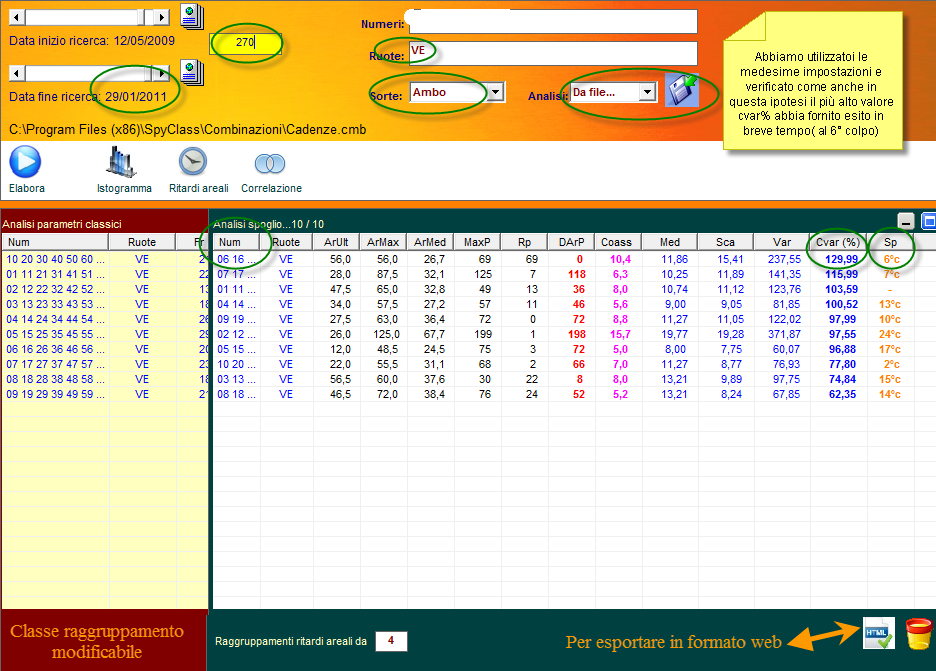
Spostiamoci come data di fine ricerca ad inizio anno 2011 e verifichiamo nel range di 180 estrazioni a ritroso se il cvar% più  basso abbia fornito esiti in breve tempo.

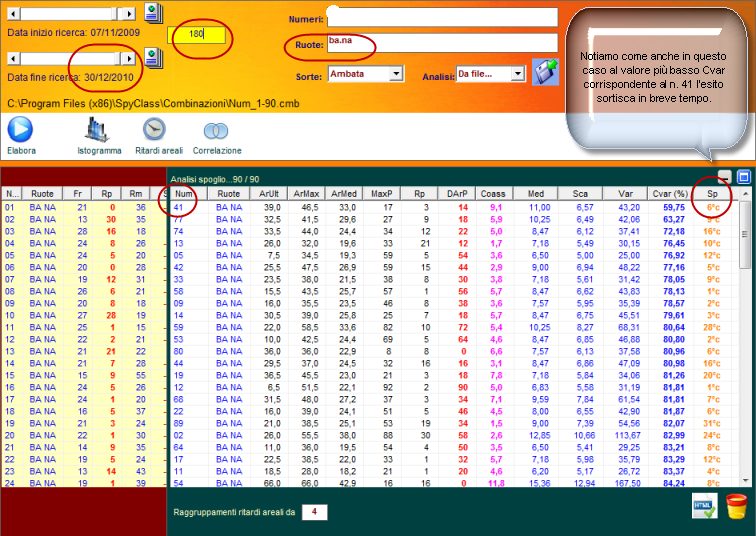
Avete visto come sia eccellente questo modello previsionale? Altri se ne possono creare tutti di ottima fattura, essendo necessario osservare i valori assunti da quell'indice in base al quale vogliamo creare il modello previsionale: ArUlt, Armax, ArMed, Darp, Coass, Sca etc. Possiamo anche valutare coppie o triple di questi indici per definire un modello previsionale di tutto rispetto, e ciò varrà per qualunque sorte d'analisi.

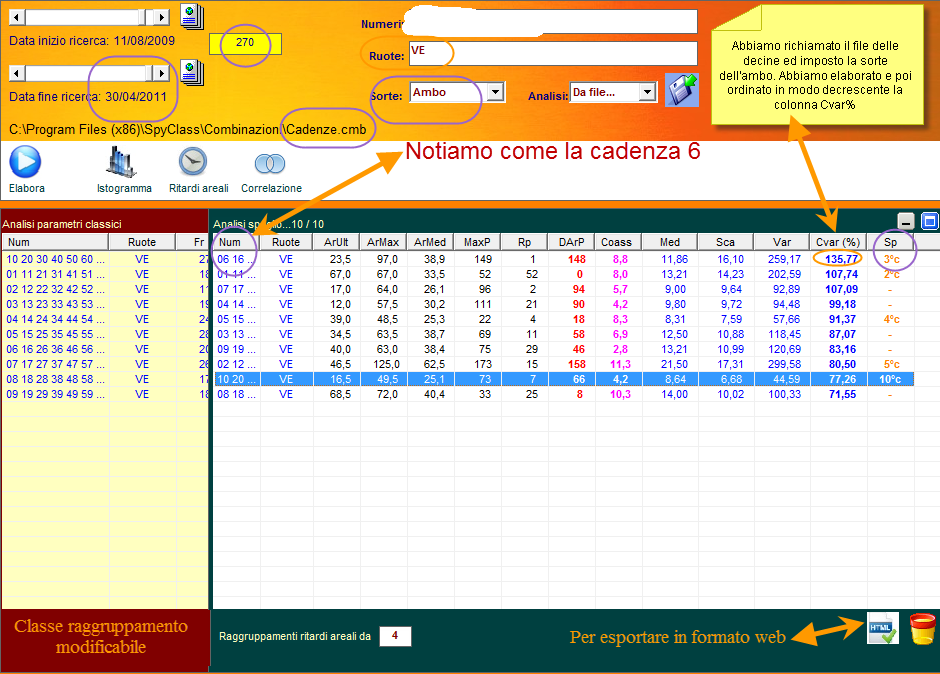
Spostiamoci come data di fine ricerca a fine gennaio 2011 e verifichiamo il modello, utilizzando gli stessi parametri della analisi di cui sopra. RICORDIAMO COME SIA IMPORTANTE LA OMOGENEITA' DELLE VARIABILI ONDE POTER ESEGUIRE COMPARAZIONI OGGETTIVE.

Capirete che in base a queste esemplificazioni come sia possibile creare processi previsionali della natura più diversa, dipendendo gli stessi da tante variabili, come i concorsi di analisi, il tipo di indice che viene posto come centro dell'analisi, la tipologia della combinazione, la sorte esaminata, la ruota. Sono praticamente illimitate le possibilità, e parimenti aggettivabili i modelli.

Il valore Coassiale

Andiamo sul più difficile e dimostriamo come il valore coassiale (Colonna Coass) possa fornirci spunti per il gioco di un singolo numero su ruota unica.
Il valore coassiale esprime il legame fra grandezze accomunate ad altre per via della condivisione di un medesimo asse. Tale valore palesa la comunanza fra valori di ritardo diversi , distinti da spazi e intercapedini diverse, una specie di isolante, ma viaggianti sul medesimo asse. La sintesi è un indice apparentemente semplice, ma che compendia in se stesso una serie di calcoli estremamente complessi.
Vediamo un modello previsionale basato sul valore coassiale e che prende in analisi i 90 numeri su ruota singola.

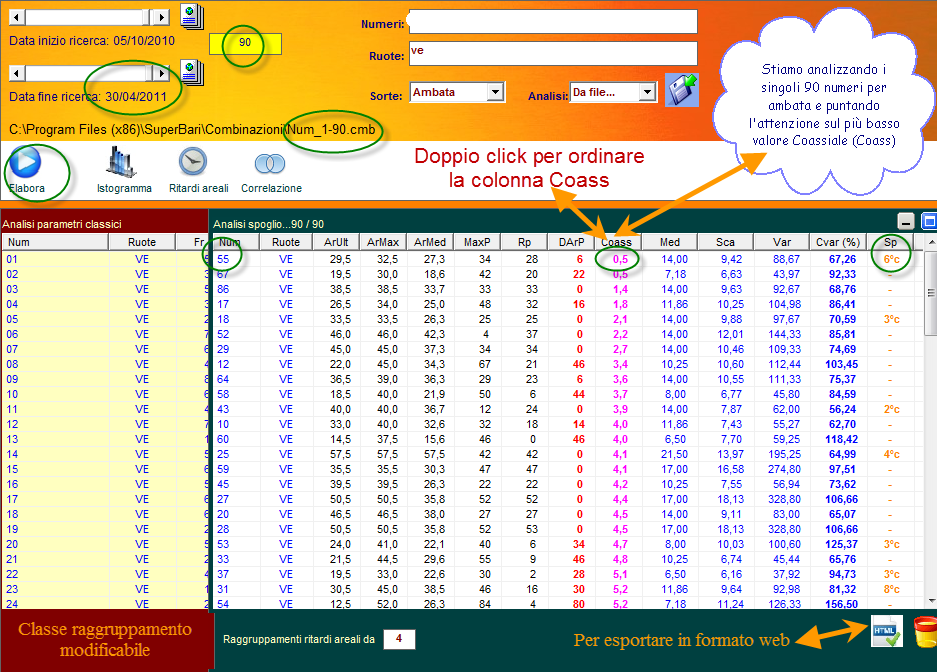
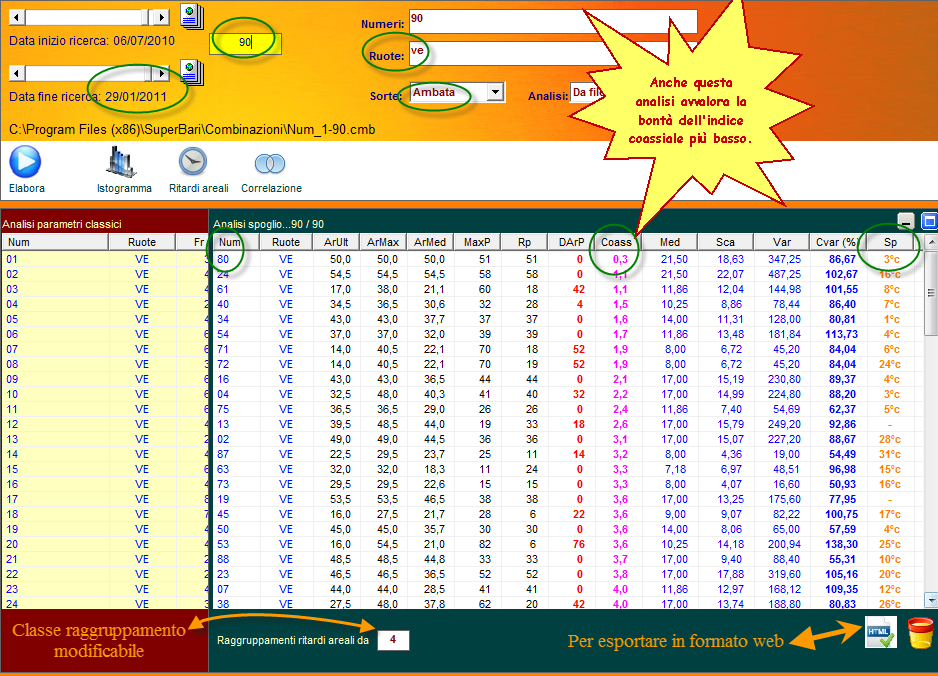
Come avrete modo di constatare, in entrambi i casi l'ambata secca su ruota singola, avente il valore coassiale più basso abbia prodotto l'esito in tempi velocissimi. Immaginatevi come sia possibile, utilizzando questo criterio, addivenire al computo di abbinamenti per ottenere l'ambo secco: basterà rimirare i diversi indici e, dopo averne preso uno come base, intercettare quello che in più riprese si sia abbinato al capogioco. L'ambo secco non rimarrà solo un miraggio, ma un probabile accadimento.

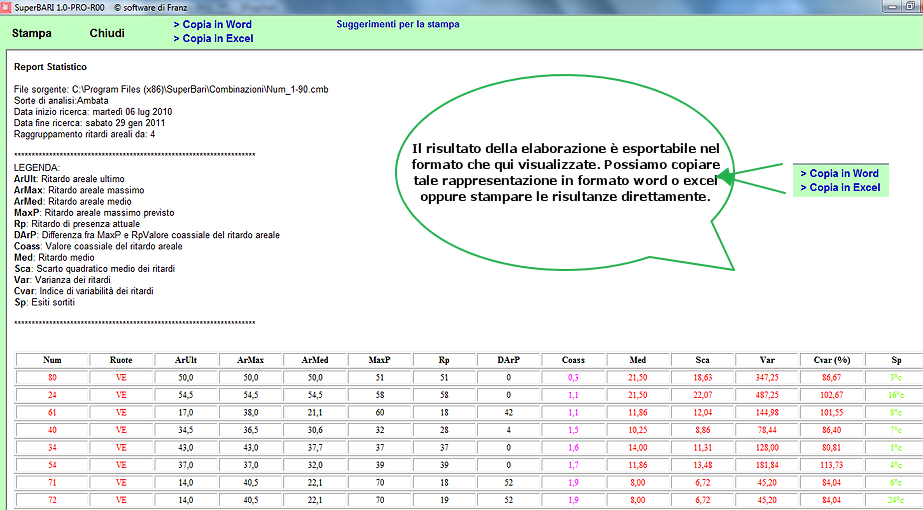
Le classi di raggruppamento e le correlazioni statistiche

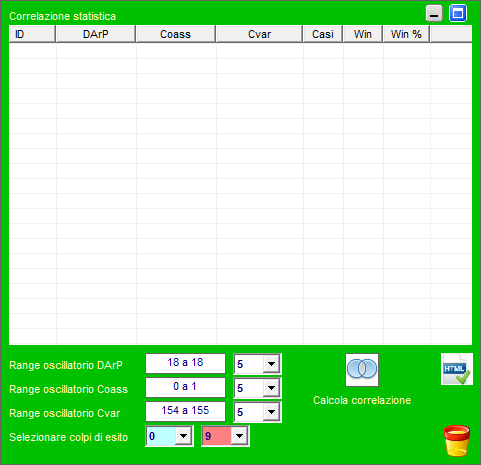
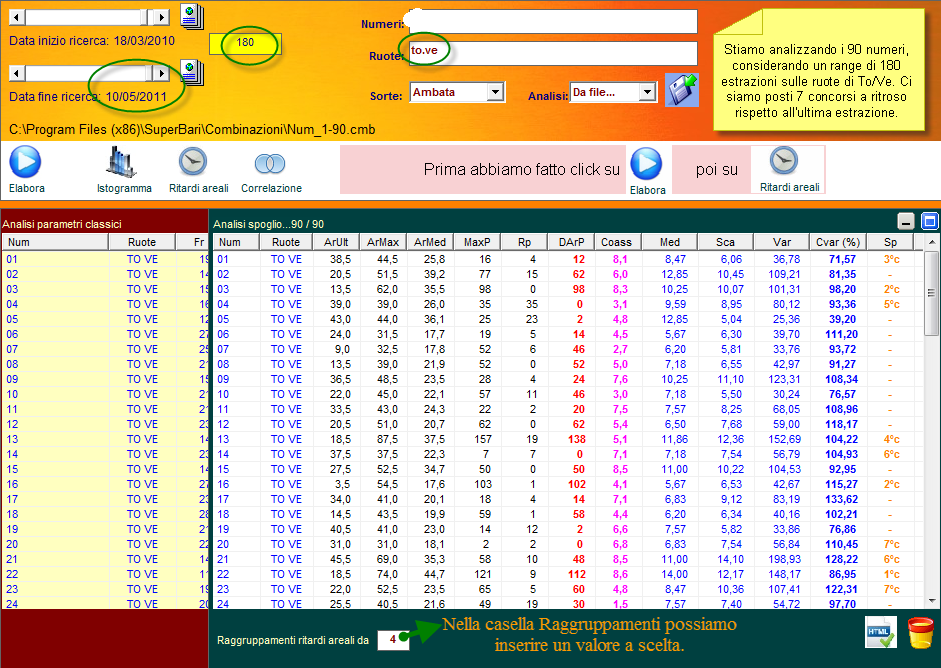
Nella parte bassa della sezione PlugStat troviamo una casellina a discesa dalla quale possiamo scegliere la forma di raggruppamento dei ritardi: da 1 a 1, da 2 a 2, da 3 a 3, da 4 a 4,....al numero da noi desiderato. In sostanza, avendo una serie di ritardi di una combinazione, poniamo 20, possiamo calcolare le statistiche avanzate considerando i 20 ritardi suddividendoli in gruppi da 2 a 2 , da 3 a 3 fino in gruppi da 20 a 20. La modifica di questo parametro restituisce risultati diversi degli indici aprendoci la strada a nuovi ed entusiasmanti modelli previsionali. Infatti, per talune combinazioni, come le ottine, potrebbero andar bene raggruppamenti bassi, a 2 a 2 oppure a 3 a 3: basta provare e ricercare, come abbiamo ampiamente discusso negli esempi precedenti, il più adeguato modello previsionale. Se ciò non bastasse potremo far uso delle correlazioni statistiche. Tale funzione si attiva cliccando sul pulsante omonimo, dopo aver proceduto alla elaborazione. QUINDI, PRIMA SI ELABORA, POI SI PIGIA SU RITARDI AREALI E, INFINE, SUL TASTO CORRELAZIONE.

Clicchiamo sulla icona "Correlazioni"e ...

Teniamo presente che le caselle che racchiudono i raggruppamenti in classi possono assumere valori diversi,non necessariamente eguali. Qualora si setti a 1 il valore delle classi, significherà che l'indice indicato nella prima casella verrà preso nella sua interezza. In sostanza rappresenterà un valore globale fisso, mentre gli altri due potranno assumere livelli diversi.

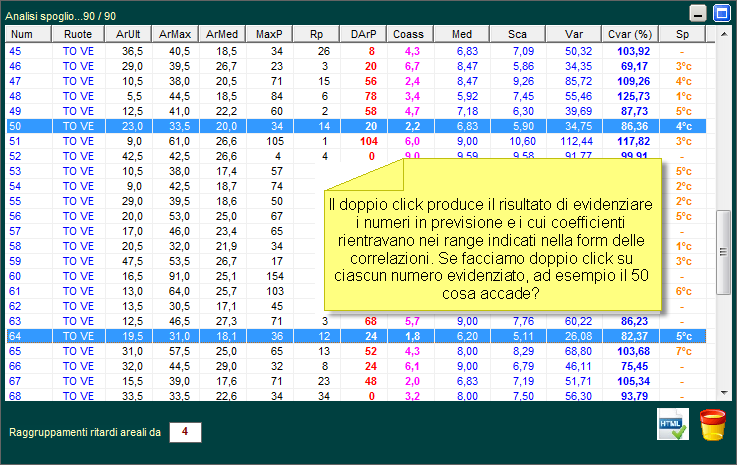
Vi chiederete: come si potrà sfruttare questa routine?

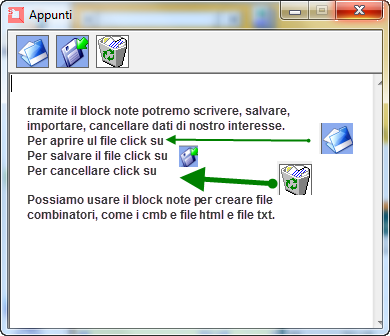
Dobbiamo, in primis, tenere a mente che la correlazione è un concetto statistico che applichiamo al lotto in quanto le variabili legate ai vari tipi di ritardo sono di natura casuale. Una serie di dati, (i vari tipi di ritardo) vengono messi in relazioni tra di loro al fine di scoprire un legame, un nesso tale che possa determinare un modello previsionale valido. Posso, ad esempio, riscontrare una correlazione tra un valore coassiale alto, e comunque entro un certo range, rispetto ad un valore DArP basso e pur esso entro un certo range. La correlazione, ovviamente, andrà valutata applicando un modello a diversi blocchi estrazionali. Nell'esempio proposto, dopo aver individuato il range per ciascun valore, DArP, Coass e CVar, che poi abbia portato ad un esito fausto, posso scrivermi i valori dei range stessi utilizzando la meravigliosa utility degli "Appunti". Essa è un block note avanzato che ci permette di scrivere dati work in progress (Nel mentre stiamo lavorando). I dati trascritti nel block note andremo ad applicarli a analisi basate su diversi blocchi estrazionali, in modo da verificare se ci sia corrispondenza. Riscontrare un legame significherà che abbiamo intercettato un modello previsionale valido ed applicabile anche alle previsioni future.

Il block note è un utile strumento che serve oltre a memorizzare i dati che ci interessa, al momento salvare, anche per creare al volo file cmb, oppure file html. Aprire gli appunti impone il semplice click sulla icona che troviamo nel menù laterale (Voce APPUNTI).

Clicca qui ritornare al menù base principale